https://ift.tt/FDrqeZg A modification of this popular algorithm that builds clusters balanced in the number of points Equal-size clusteri...
A modification of this popular algorithm that builds clusters balanced in the number of points
Clustering is a methodology used to group data points containing similar features among them. It is broadly used in exploratory data analysis and it has proven to be very important in many applications such as pattern recognition, market and customer segmentation, recommendation systems, data compression, and biological data analysis, among others.
Despite the extensive number of clustering algorithms, none of them generate clusters balanced in the number of points. Such equal-size clusters are very important in some fields, for instance, in the last-mile delivery sector where a large number of orders can be aggregated into equal-size groups with the aim to improve the delivery routes and to maximize vehicle capacity utilization.
Given the need to have an equal-size clustering, a few colleagues and I expanded the so-called spectral clustering to generate clusters balanced in the number of points. This new algorithm constructs clusters — with a similar number of points — based on the geographical information of the data points.
The full code can be found in this GitHub repository. It is meant to contribute to the data science community. Give it a try if you need to create equal clusters of points on a map!
Equal-size spectral clustering: The algorithm
The equal-size clustering is composed of three steps: Cluster initialization, computation of each cluster’s neighbors, and balancing the points in each cluster. Let’s review each of them in detail.
Clustering initialization
In the first step, we create clusters by using Scikit-learn’s implementation of the spectral clustering algorithm. Spectral clustering is very powerful at aggregating spatial data because it identifies communities of nodes in a graph based on the edges connecting them. The spectral clustering algorithm is particularly useful at clustering points that follow a circular symmetry. If you are interested in knowing more about this method, you can read this awesome post written by William Fleshman:
There are two hyperparameters needed to do the cluster initialization: nclusters, which is the number of desired clusters, and nneighbors, which is the number of neighbors per data point. This last parameter is used by spectral clustering to construct the affinity matrix. Good values of nneighbors are between 7% and 15% of the data points.
Computation of each cluster’s neighbors
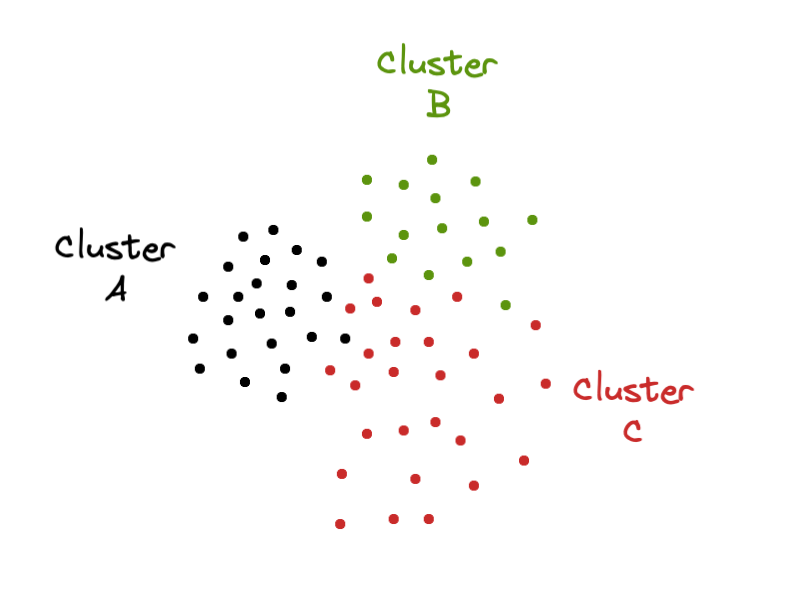
Once the clusters are created, the second step of the algorithm is computing each cluster’s neighbors. How is this calculation made? By estimating the mode of the cluster labels of every data point’s nearest neighbors. For example, if point x belongs to cluster A and the majority of its nearest neighbors belong to cluster B means that cluster B is a neighbor of cluster A.
The computation of each cluster’s neighbors is extremely important because the balancing of clusters is made by exchanging points among neighboring clusters.

Balancing the points on each cluster
The last step of the algorithm is balancing the points on each cluster. As explained above, we do that by exchanging points among neighboring clusters. Big clusters transfer points to smaller neighboring clusters. In the balancing, we aim at making the cluster sizes roughly equal to N / ncluster, where N is the total number of data points.
To balance the clusters in size, we define the hyperparameter equity_fraction. The equity_fraction is a number defined in the interval (0,1] and it constrains how equal the resulting clusters must be. If equity_fraction is zero, the clusters will keep the same initial size. Ifequity_fraction is one, the resulting clusters will have sizes roughly equal to N / ncluster.

Let’s make a small parenthesis to define a quantity called cluster dispersion. Cluster dispersion is defined as the standard deviation of the points’ distances within a cluster. You can think of it as a slightly modified version of the within-cluster distance.
The equity_fraction affects the initial cluster dispersion because the exchange of points increases the distances among the points within a cluster. In this case, I advise you to use an optimization algorithm to find the optimal cluster hyperparameters that minimize cluster dispersion. In the next section, I mention how you can get the cluster dispersion out of the Python code.
Other functionalities
It is important to remember that equal-size spectral clustering can be used to create aggregations of spatial points. The repository comes with a plotting functionality that can be used in cases where you have the coordinates of the data points. In the next section, we’ll see this functionality in action.
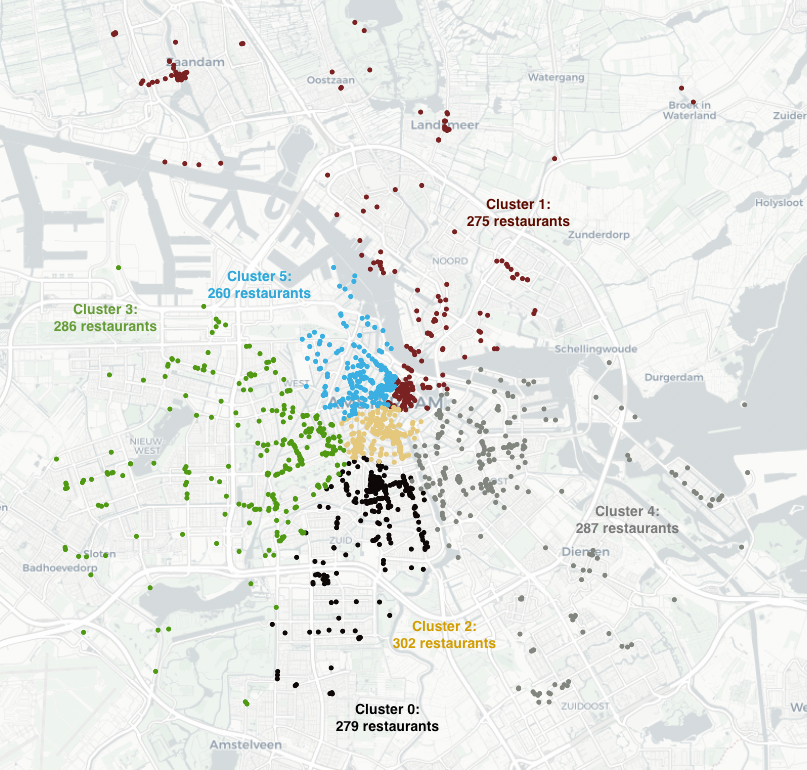
Use case: Clustering of restaurants in Amsterdam
Imagine that you are the owner of a farm in The Netherlands and you want to deliver your fresh high-quality food to a large fraction of restaurants located in Amsterdam. You have 6 vehicles with the same capacity, which means that they are able to deliver roughly to the same amount of restaurants.
In order to fully utilize the capacity of the vehicles, you can use equal-size clustering to group the restaurants such that every vehicle does not travel too much from one restaurant to another.
Let’s first read the location of the restaurants:
The file restaurants_in_amsterdam.csv contains a list of restaurant locations within a distance of 8 km around Amsterdam’s central station. You can find this file in the folder datasets in the GitHub repository.
From the locations listed in the coords data frame, it’s possible to estimate a matrix that contains the travel distance between each pair of points. The shape of this matrix is (n_samples, n_samples), and it must be symmetric. This matrix is the input received by the equal-size clustering.
Now we can run the equal-size spectral clustering. It’s as easy as calling the class SpectralEqualSizeClustering:
In this example, we create 6 clusters. We select the number of neighbors nneighbors to be 10% of the number of points in the input dataset. As we want clusters as equal as possible, we set the equity_fraction to 1.
You can see how the cluster label of each data point is obtained by calling the fit method. Important note: A function to predict the cluster labels for points that weren’t in the original data is not implemented yet. I encourage you to develop this functionality if you find this code useful for your work!
The cluster labels obtained above can be added to the data frame coords to plot the resulting clusters on a map:
By running the code above, we obtain an interactive plot containing all the clusters, as shown in the figure:

In that plot, you can select each cluster to visualize it separately:
The optimization of hyperparameters was not needed in the use case explained above. However, as I mentioned before, it is possible to use an optimization method if required. In this case, you can use as an optimization metric the attribute clustering.total_cluster_dispersion, which is the sum of all cluster dispersions. By minimizing this quantity, the resulting clusters will be more compact.
Take home messages
In this blog, I presented a modification of the spectral clustering code that generates clusters balanced in the number of points. This algorithm can be used to generate equal aggregations of spatial points, and it might also be useful in improving some processes in the last-mile delivery sector.
Important considerations of equal-size spectral clustering are the following:
- The input data must be a symmetric distance matrix associated with the coordinates of the data points.
- The hyperparameters of the clustering code are the number of desired clusters (nclusters); the number of neighbors per data point (nneighbors), and a fraction that determines how equal in size the clusters must be (equity_fraction). You can use any optimization algorithm to find the best parameters that minimize the total cluster dispersion (total_cluster_dispersion).
- The equal-size clustering might be used for non-spatial data as well, however, it has not been tested for this purpose. If you want to experiment with it, define a metric to create the symmetric distance matrix that is needed by the code as input. Be sure to normalize or standardize your variables first.
- The code doesn’t have a prediction method yet, but you are welcome to contribute if you find this code useful.
I hope you enjoyed this post. Once more, thanks for reading!
Credits: The equal-size spectral clustering was developed in collaboration with Mor Verbin, Lilia Angelova, and Ula Grzywna. Such an amazing data team!
Equal-size spectral clustering was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium
https://towardsdatascience.com/equal-size-spectral-clustering-cce65c6f9ba3?source=rss----7f60cf5620c9---4
via RiYo Analytics

No comments