https://ift.tt/3eOuYrU Efficient Clinic Flow and Reduced Wait Times Image by Anna Dziubinska on Unsplash One of the most foundational ...
Efficient Clinic Flow and Reduced Wait Times

One of the most foundational experiences for both patients and providers is clinic flow and optimization. Research shows that continuity of care, which is the seamless service through integration, coordination and sharing of information between providers, improves health outcomes and lowers cost [1]. Continuity of care is particularly important for patients with high utilization, that require multiple, integrated services, like chemotherapy.
However when priorities and needs are constantly changing, coordination becomes that much more difficult, and any inefficiencies can become exponential.
Let’s explore this a little further through some mixed integer programming.
Can we optimize patient throughput?
We can get pretty close. One solution exists outside of healthcare, another industry with similar problems: consumer supply chains.
In the 1970s, the math behind mixed integer programming (MIP) made it possible to maximize production given a set of financial, storage, and delivery constraints (think crop production). Then in the 1990s, computing expanded the number of allowable constraints, providing more specific solutions. By 2012, several researchers began applying these methods to patient scheduling [2–6]. Today, new Python packages can leverage MIP to create schedules that meet unique clinical demands.
Patient Scheduler Program V1
Below, I’ll layout a first iteration of a patient scheduler that I designed using the PuLP library. The primary objective will be to shorten the work day (makespan) by optimally arranging appointments, of various types and durations, without overlap.
As a visual of what we’re trying to achieve, a naive scheduler might take 5 patients and book them this way:

An optimized scheduler would take the same 5 patients and effectively condense a 24-hour day to just 10 hours:

The important features of scheduling are preserved because patients (1) are only seen in one place at a time, (2) can have some or all of these visits, (3) in any order needed, (4) for any time needed.
So how can we build this model for any number of patients and visits?
Transforming Mixed Integer Programming into Python
Mathematically, this is an NP-hard problem that uses Mixed Integer Programming. Integer programming attempts to find optimal arrangements for given variables that satisfy constraints (really functions) while also either maximizing or minimizing some objective function. In our case, our objective function is to shorten the total workday. I’ll also outline the appropriate variables and constraints below.
Import Package
# import PuLP library for Mixed-Integer Programming
from pulp import *
Input Data
We need to define upfront our known number of patients, their visit types and appointment durations.
Let’s take 5 patients with this schedule as our example:
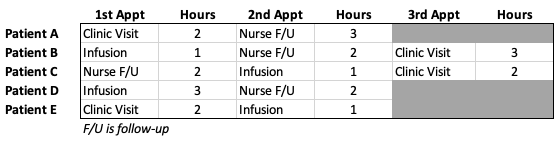
Note the patients have different types of visits, of varying order and duration. In this example, we are using between 2–3 visits per patient in a single day. However, the code below is flexible to support a variety of permutations.
In Python, we can transform the above schedule into the following matrices:
# define number of visit types and patients
visits = 3
patients = 5
# visit duration for each patient
times = [[2, None, 3],
[1, 2, 3],
[2, 1, 2],
[None, 3, 2],
[2, 1, None]]
# the order each visit will occur
clinic_sequence = [[0, 2],
[1, 2, 0],
[2, 1, 0],
[1, 2],
[0, 1]]
# some large number
M = 100
The list rows are the patients. The variable clinic_sequence above specifies the visit order, where 0 = clinic visit, 1 = infusion, and 2 = nurse follow-up. The times are the durations, corresponding to each visit type. M is just a big number, which will be used to satisfy one of the constraints below.
Convenience Variables
We can also create a few convenience variables that will be used later in the constraint functions. The first of variable will notate all permutations of patient and visits. We’ll call this valid_starts.
# the combo of patients and visits actually needed
valid_starts = [(j, m) for j in range(patients) for m in clinic_sequence[j]]
valid_starts.sort()
The second convenience variable will be called jjm. This represents patients (j), prior patients (j_prime), and visits (m), where j will never be a j_prime. The reason this distinction is important is because visits can only accommodate one patient at a time.

So this will serve as our binary variable. Below we’ll plug this into a constraint that ensures only one patient is being seen at a time. But for now, we can think of this as all the patient-patient-visit combinations.
# define a variable called jjm
# the relevant patient-patient-visit combos
jjm = [(j, j_prime, m)
for j in range(patients)
for j_prime in range(patients)
for m in range(visits)
if j != j_prime
and (j, m) in valid_starts
and (j_prime, m) in valid_starts]
Objective Function
Leveraging the PuLP library, we can create a model called schedule that will operate to minimize the day’s makespan.
# define the model to minimize the workday
schedule = LpProblem(name="Minimize_Schedule", sense=LpMinimize)
Variables
We can then assign the convenience variables into the scheduler model as dictionaries that hold all the relevant permutations. We’ll use: x, y and c.
- x will be a dictionary of all valid_starts. It can never be <0, so lowbound=0. It’s continuous.
- y will be a dictionary of jjm. Remember, this will operate to ensure one patient goes at a time, and not at the same time. It’s binary.
- c will be the entire workday duration. The lowbound=0. It’s continuous.
# continuous x = the start time, for all valid_starts
# x[j, m]
x = LpVariable.dicts("start_time", indexs=valid_starts, lowBound=0, cat="Continuous")
# binary y = that patient j precedes patient j_prime on visit m
# y[j, j_prime, m]
y = LpVariable.dicts("precedence", indexs=jjm, cat='Binary')
# workday variable to capture the shortest makespan
c = LpVariable("makespan", lowBound=0, cat='Continuous')
Constraints
Next, we will need to define a few constraints.
The first constraint must be a precedence constraint, which ensures that a visit cannot begin until the last one ended. Mathematically, it looks like this:
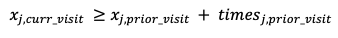
Where curr_visit is the range of all visits for each patient (except the first one because there is no visit before the first visit), and prior_visit which is just the first prior visit from all visits for each patient.
In Python, we can add this logic to the schedule model like so:
### visit sequence constraint ###
for j in range(patients): #for each patient
for m_idx in range(1, len(clinic_sequence[j])): #for each visit sequence (except first one)
curr_visit = clinic_sequence[j][m_idx]
prior_visit = clinic_sequence[j][m_idx - 1]
# add constraint to the model
schedule += x[j, curr_visit] >= x[j, prior_visit] + times[j][prior_visit]
The second constraint we’ll call a single-use constraint. Basically, this ensures that a patient is only in one visit, at one time. We can apply the big M constant to ensure the correctness of this constraint.
So if y=1, we know patient j_prime will precede patient j, and big M permits patient j_prime to come first. If y=0, then we know patient j precedes patient j_prime, and no big M applied will allow patient j to come first.
Mathematically this can be written as:
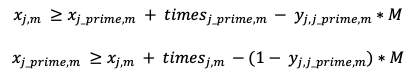
In Python, this can be translated to:
### single-use constraint ###
for j, j_prime, m in jjm:
# if y=1, then patient j_prime precedes j, and apply big M
# if y=0, then patient j precedes j_prime, and do not apply big M
schedule += x[j, m] >= x[j_prime, m] + times[j_prime][m] - y[j, j_prime, m]*M
schedule += x[j_prime, m] >= x[j, m] + times[j][m] - (1-y[j, j_prime, m])*M
The final constraint ensures that the entire makespan is computed correctly. The makespan has to be at least as big as all patient visit start times plus their corresponding durations.
### constraint to capture longest makespan ###
schedule += c # put objective function into model
for j, m in valid_starts:
schedule += c >= x[j, m] + times[j][m]
Solve the Model
Call solve on your model to apply the constraints and variables to see if there is an optimal schedule.
status = schedule.solve()
Show the Results
Then we can print the results, and see if there is an optimal solution, along with when each patient will start at each visit.
print(f"status: {schedule.status}, {LpStatus[schedule.status]}")
print("Completion time: ", schedule.objective.value())
for j, m in valid_starts:
if x[j, m].varValue >= 0:
print("Patient %d starts in clinic %d at time %g" % (j+1, m, x[j, m].varValue))
There is an optimal solution here, with the entire day spanning only 10 hours.
The output is:
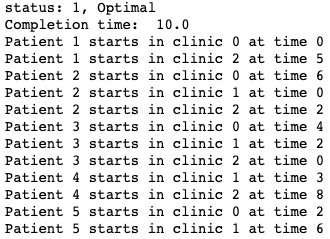
Creating a V1 Graphical Scheduler
We need to translate this into a visual representation to more easily see which patients go where, and when.
We can do this by writing a good deal of code.
# create full list of start times
start_times = []
for j, m in valid_starts:
if x[j, m].varValue >= 0:
start_times.append(x[j,m].varValue)
# create full list of durations
duration = []
for time in times:
for i in time:
duration.append(i)
duration = [x for x in duration if x is not None]
# create full list of visits
visits = []
for j, m in valid_starts:
if x[j, m].varValue >= 0:
visits.append(m)
visits
# create full list of patients
patients = []
for j, m in valid_starts:
if x[j, m].varValue >= 0:
patients.append(j)
patients
# create the indexes for all visits
machine_1 = [i for i,e in enumerate(visits) if e ==0 ]
machine_2 = [i for i,e in enumerate(visits) if e ==1 ]
machine_3 = [i for i,e in enumerate(visits) if e ==2 ]
Then we can leverage the matplotlib library to actually make the schedule using the new variables from above.
import matplotlib.pyplot as plt
fig, gnt = plt.subplots()
# set axes names
gnt.set_xlabel("Time (in hours)")
gnt.set_ylabel("Clinic Visit")
# set axes ranges
gnt.set_ylim(9,40)
gnt.set_xlim(0, schedule.objective.value())
# Setting ticks on x-axis
gnt.set_xticks([1,2,3,4,5,6,7,8,9,10])
# set the y tick-labels
gnt.set_yticklabels(['Clinic Visit', 'Infusion', 'Nurse Follow-Up'])
gnt.set_yticks([15,25,35])
# Setting graph attribute
gnt.grid(True)
colors_1 = []
for idx in [patients[x] for x in machine_1]:
if idx == 0:
colors_1.append("tab:green")
if idx == 1:
colors_1.append("tab:orange")
if idx == 2:
colors_1.append("tab:blue")
if idx == 3:
colors_1.append("tab:purple")
if idx == 4:
colors_1.append("tab:red")
ncolor= 0
for idx, val in enumerate(machine_1):
try:
gnt.broken_barh([([start_times[x] for x in machine_1][idx],[duration[x] for x in machine_1][idx])], (10,9), facecolors=colors_1[ncolor])
ncolor+=1
except IndexError:
pass
colors_2 = []
for idx in [patients[x] for x in machine_2]:
if idx == 0:
colors_2.append("tab:green")
if idx == 1:
colors_2.append("tab:orange")
if idx == 2:
colors_2.append("tab:blue")
if idx == 3:
colors_2.append("tab:purple")
if idx == 4:
colors_2.append("tab:red")
ncolor= 0
for idx, val in enumerate(machine_2):
try:
gnt.broken_barh([([start_times[x] for x in machine_2][idx],[duration[x] for x in machine_2][idx])], (20,9), facecolors=colors_2[ncolor])
ncolor+=1
except IndexError:
pass
colors_3 = []
for idx in [patients[x] for x in machine_3]:
if idx == 0:
colors_3.append("tab:green")
if idx == 1:
colors_3.append("tab:orange")
if idx == 2:
colors_3.append("tab:blue")
if idx == 3:
colors_3.append("tab:purple")
if idx == 4:
colors_3.append("tab:red")
ncolor= 0
for idx, val in enumerate(machine_3):
try:
gnt.broken_barh([([start_times[x] for x in machine_3][idx],[duration[x] for x in machine_3][idx])], (30,9), facecolors=colors_3[ncolor])
ncolor+=1
except IndexError:
pass
plt.grid(True)
gnt.plot()
And here are our 5 patients, each their own color, scheduled in such a way that optimizes the entire workday as much as possible.
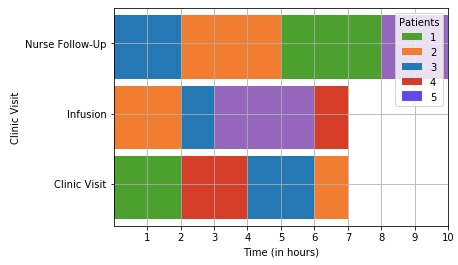
Next Steps
In pursuing a V2 of this model, there are a few obvious areas to consider.
- This model’s priority is to make the shortest provider workday possible, not necessarily the shortest patient wait times. See above: Patient 2 (orange) goes directly to a clinic visit from their infusion, but then has to wait 1 hour until his nurse follow-up. In a more ideal world, both patient and provider move through without waits until the shortest possible day is over.
- The schedule graph itself is very simple and not super dynamic. The code could be simplified to achieve better scalability.
- While the model can accommodate patient “no-shows,” visits that run long or end early can not be integrated.
- As mentioned earlier, the input data are matrix data. In production, scheduling staff would never enter data this way. Ideally, we would build a proper UI to enable data entry (i.e. text fields, drop-downs, search, etc.) via a method such as Flask and SQLAlchemy. Their inputs could then transform to the matrix under the hood.
Thanks for reading! Feel free to connect with me on LinkedIn for any questions or suggestions for future articles. I look forward to connecting with others who work at the intersection of data and healthcare operations.
Citations
[1] What is ‘Continuity of Care’? Gulliford, M., Naithani, S., Morgan, M. J Health Serv Res Policy. 2006 Oct;11(4):248–50. Web: https://pubmed.ncbi.nlm.nih.gov/17018200/
[2] Issabakhsh, M., Lee, S., Kang, H. (2018). A Mixed Integer Programming Model for Patient Appointment in an Infusion Center. Proceedings of the 2018 IISE Annual Conference. Abstract ID: 2061.
[3] Turkcan, A., Zeng, B., & Lawley, M. (2012). Chemotherapy operations planning and scheduling. IIE Transactions on Healthcare Systems Engineering, 2(1), 31–49. 10.
[4] Tanaka, T. (2011). Infusion chair scheduling algorithms based on bin-packing heuristics. State University of New York at Binghamton. 11.
[5] Castaing, J., Cohn, A., Denton, B. T., & Weizer, A. (2016). A stochastic programming approach to reduce patient wait times and overtime in an outpatient infusion center. IIE Transactions on Healthcare Systems Engineering, 6(3), 111–125. 12.
[6] Sadki, A., Xie, X., & Chauvin, F. (2011, August). Appointment scheduling of oncology outpatients. In Automation Science and Engineering (CASE), 2011 IEEE Conference on (pp. 513–518). IEEE.
Optimizing Patient Scheduling was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3pRuZle
via RiYo Analytics

ليست هناك تعليقات