https://ift.tt/3yRCRpC I struggled to understand the Fourier transform until I mapped the concept onto real-world intuitions. This is the f...
I struggled to understand the Fourier transform until I mapped the concept onto real-world intuitions. This is the first article in a series of increasingly technical explanations. I hope the intuitions help you, too!
Sound is a mechanical wave, a vibration in the air or another medium. Musical notes correspond to the frequency of the wave. A high frequency wave corresponds to a high note (more rapid changes between high and low pressure), and a low frequency wave corresponds to a low note (slower changes between high and low pressure).
These waves propagate through space over time. As a wave reaches a microphone, it wiggles a structure called the diaphragm. The movement of the diaphragm generates an electrical current, which allows us to record the rate of pressurization and depressurization.
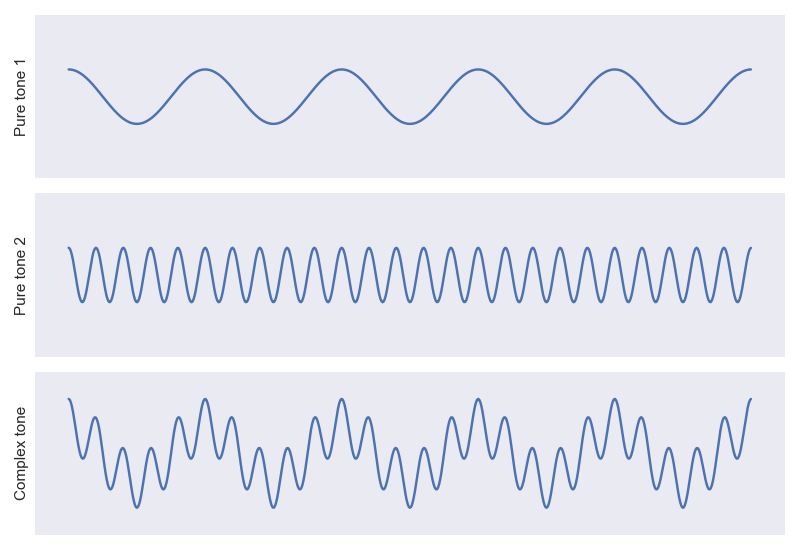
If we consider a stationary microphone as a wave passes it, the recorded change in pressure is a function of time. This representation in the temporal domain plays nicely with our intuitions: as time progresses, pressure increases and decreases periodically at a rate corresponding to the frequency. More complex tones are a summed combination of multiple frequencies (Figure 1).
This representation of the signal in the time domain is dense: it is non-zero for most of the domain. But we know we can talk about a musical tone more succinctly than describing the pressure at each time point. Instead, we can simply name a note or, equivalently, state the frequency in hertz (Hz): the number of cycles per second.
In the frequency domain, the x-axis represents frequency and the y-axis is the amount of the frequency in the signal. For the simple tones described in Figure 1, this description in the frequency domain is sparse: it is zero for most of the domain.
The Fourier transform is the mathematical operation that maps our signal in the temporal or spatial domain to a function in the frequency domain.
The Fourier transform does exactly what we want! It takes the dense temporal signals we plotted in Figure 1 and gives us Figure 2’s sparse description in the frequency domain. Each of the component frequencies is obvious looking at the plots.
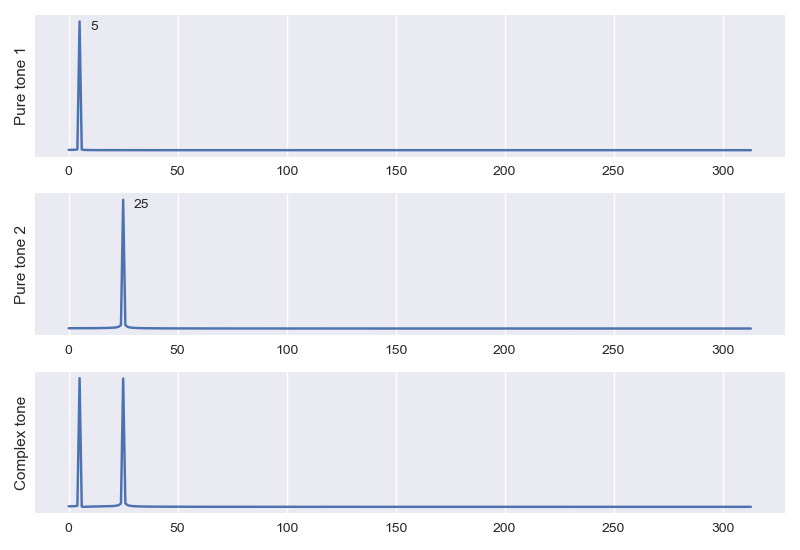
If we consider the temporal duration of the signals from Figure 1 as one second, the x-axis values in Figure 2 correspond to hertz. The Fourier transform recovers 5Hz for the first plot, 25Hz for the second, and a combination for the third complex tone. For all other frequency values, the Fourier transform is approximately zero-valued. For now, we are only considering magnitude, we will explore more in later posts!
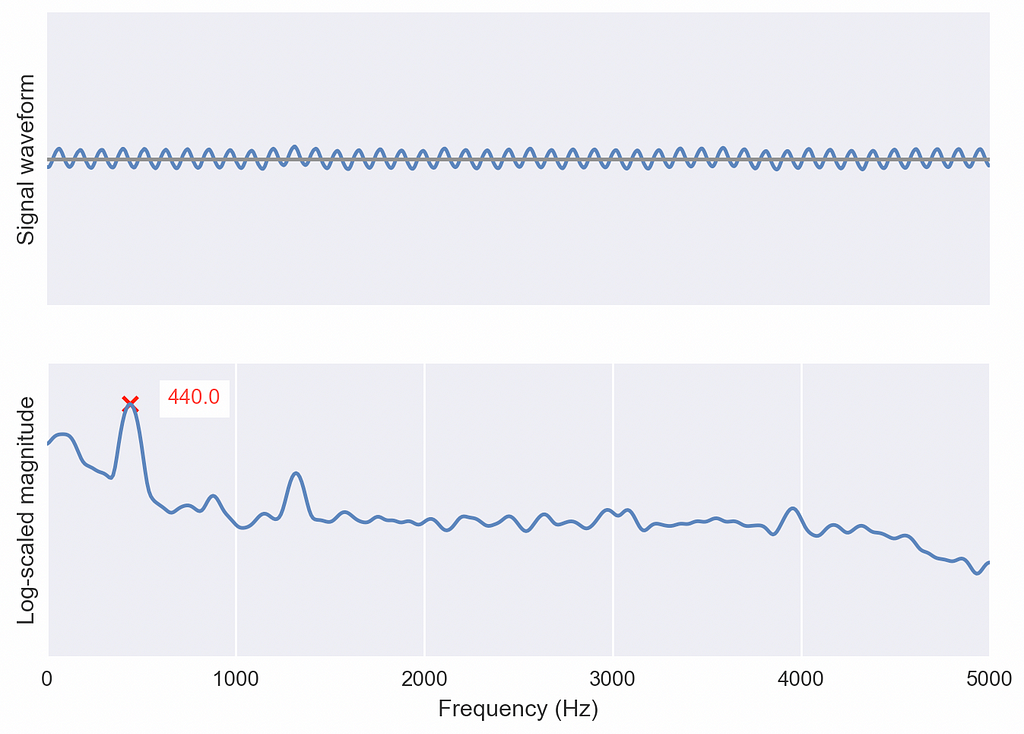
I’ve found it most valuable to experiment with the Fourier transform on realtime audio data! I put together a small Python repository to experiment with the results of a Fourier transform applied to short snippets recorded from a computer microphone.
Check out the source! Experiment with instruments and environmental sounds.
Understanding-Fourier/fourier_1 at master · peterbbryan/Understanding-Fourier
Give the article a clap if the repo or text were valuable to you! Leave a comment if you’ve encountered other metaphors that helped you understand a mathematical concept.
If folks are interested, I look forward to writing increasingly technical summaries of the Fourier transform! Thanks for reading!
The Fourier Transform (1): Introduction to the frequency domain was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/33Ki4bW
via RiYo Analytics

ليست هناك تعليقات