https://ift.tt/3FeDonr Learn how to evaluate it computationally and analytically, leveraging the power of JAX ! Photo by David Sjunnesso...
Learn how to evaluate it computationally and analytically, leveraging the power of JAX!

Intro
Suppose you have a random variable X, and you put it through some transformation g. The distribution of the resulting random variable g(X) is known as the “pushforward distribution”. Today we’ll learn how to calculate its probability density.
Example
Rather than talking abstractly, let’s start with a practical example. Let’s consider a 2D random variable X
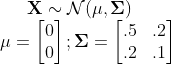
and transformation g
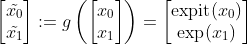
which we’ll apply to it. X will get transformed by g into g(X), and we want a formula for the probability distribution of g(X).
Preliminaries
Let’s import what we need, define our distribution, and define our transformation.
Great. To compute g(X), we just need to:
- extract samples from distribution
- apply g to each element of samples
(if you’re not familiar withjax.vmap- see jax vectorisation - don’t worry, it’s just a trick to vectorise computation)
We can then take a look at how the probability density of X changes under g:

That’s our pushfoward distribution! Now let’s see how to calculate it analytically.
Let’s do it analytically (no maths)
Hunting around online (e.g. here), we can find a cute little formula for the pushforward probability density:

The last term involves a determinant and a Jacobian, and I don’t trust myself to calculate them correctly (especially for anything production-ready at Gousto — btw, if you want a seriously interesting DS job, we’re hiring!).
Fortunately, however, I don’t need to calculate them myself — my computer can do it for me! With JAX, evaluating the Jacobian of transformation and point is as simple as jax.jacobian(transformation)(point)! Check this out:
Once we’ve found pushforward_density, we can plot it alongside its computationally-calculated counterpart:
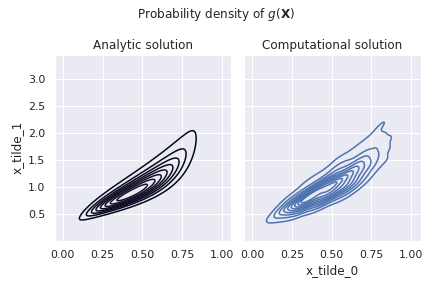
Hey, they match!
Conclusion
If we push a probability distribution through a transformation, we end up with a pushforward distribution. Here, we learned how to calculate its probability density, both computationally and analytically. Neither method required us to do any maths by hand, thanks to the awesome JAX library.
References
For more on pushforward distributions, I’d suggest reading Betancourt’s excellent Probability Theory case study.
What’s a pushforward distribution? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3ox0krw
via RiYo Analytics

No comments