https://ift.tt/3c8XDGR Non-Convex Optimization from both mathematical and practical perspective: SGD, SGDMomentum, AdaGrad, RMSprop, and Ad...
Non-Convex Optimization from both mathematical and practical perspective: SGD, SGDMomentum, AdaGrad, RMSprop, and Adam in Python

In this article, the short mathematical expressions of common non-convex optimizers and their Python implementations from scratch will be provided. Understanding the math behind these optimization algorithms will enlighten your perspective when training complex machine learning models. The structure of this article will be as follows. First I’ll talk about the particular optimization algorithm in short, then I’ll give the mathematical formula and provide the Python code. All algorithms are implemented by pure NumPy. Here are the non-convex optimization algorithms that we’ll discuss
- Stochastic Gradient Descent (SGD)
- SGDMomentum
- AdaGrad
- RMSprop
- Adam
Let’s start with the simplest one, Stochastic Gradient Descent.
Stochastic Gradient Descent (SGD)
SGD is an iterative, non-convex, and first-order optimization algorithm over the differentiable error surfaces. It is a stochastic estimation of gradient descent, in which the training data is randomized. It is a computationally-stable and mathematically well-established optimization algorithm. The intuition behind SGD is that we take the partial derivative of the objective function with respect to the parameter we can to optimize, which yields its gradient, which shows the increasing direction of the error loss. Hence, we take the negative of that gradient, to step forward where the loss is not increasing. To ensure stable and less-oscillatory optimization, we introduce the learning rate parameter ŋ then multiply the gradient with ŋ. Finally, the obtained value is subtracted from the parameter that we can optimize in an iterative fashion. Here is the SGD update formula and Python Code.
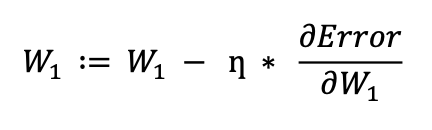
SGDMomentum
In the context of SGD, instead of computing the exact derivate of our loss function, we’re approximating it on small batches in an iterative fashion. Hence, it is not certain that the model learns in a direction where the loss is minimized. To propose more stable, direction-aware, and fast learning, we introduce SGDMomentum that determines the next update as a linear combination of the gradient and the previous update. Hence, it takes into account the previous updates also.
In general, momentum stochastic gradient descent provides 2 certain advantages over classical one:
- Fast convergence
- Less oscillatory training
Here is the formula and the Python code for SGDMomentum.
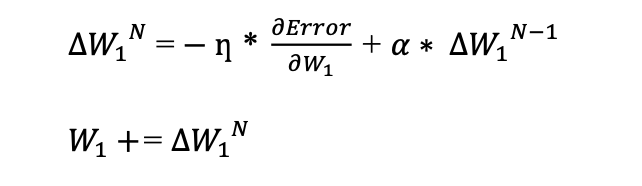
where α is the momentum coefficient which takes values in [0,1]. Alpha (α) is an exponential decay factor that determines the relative contribution of the current gradient and earlier gradients to the weight change [1]. In the case of α = 0, the formula is just pure SGD. In the case of α = 1, the optimization process takes into account the full history of the previous update.
From that point, we will move into more complex optimizers in the context of deep learning. There are some widely used optimization algorithms such as AdaGrad, RMSprop, and Adam. They are all adaptive optimization algorithms i.e., they adapt the process of learning by rearranging the learning rate so that model can reach ad-hope global minima more efficiently and faster. Here are formulas and implementations.
AdaGrad
AdaGrad optimization algorithm keeps track of the sum of the squared gradients that decay the learning rate for parameters in propagation to their update history. The mathematical expression for that:
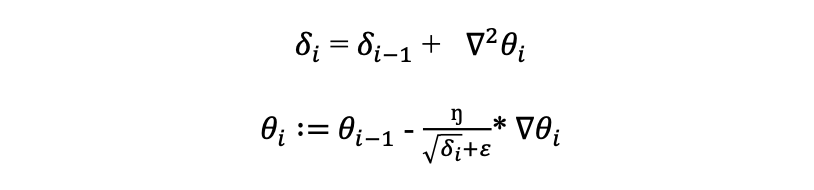
Where 𝛿𝑖 is the cumulative sum of squared gradients, ∇𝜃𝑖 is the gradient of the 𝜃𝑖 that is configurable parameters of the network and 𝜀 is the scalar to prevent zero division. When the cumulative sum increases gradually, the denominator of the update term increases simultaneously that causing a decrease in the overall update term ŋ * ∇𝜃𝑖. With the decreases √𝛿𝑖+𝜀 of the update term, AdaGrad optimization is becoming slower. Therefore, AdaGrad is stuck when close to convergence since the cumulative sum is increased gradually so that the overall update term is significantly decreased.
RMSprop
RMSprop optimization algorithms fix the issue of AdaGrad by multiplying decaying rate to the cumulative sum and enable to forget the history of cumulative sum after a certain point that depends on the decaying term that helps to convergence to global minima. The mathematical expression for RMSprop is given by:
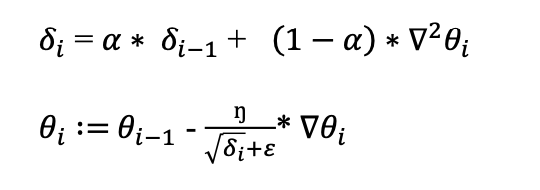
where 𝛼 is the decaying term. Therefore, this decaying term provides faster convergence and forgets the cumulative sum of gradient history that results in a more optimized solution.
ADAM
Adam optimization algorithm is the developed version of the RMSprop by taking the first and second momentum of the gradient separately. Therefore, Adam also fixes the slow convergence issue in closing the global minima. In this version of the adaptive algorithm, the mathematical expression is given by:

where 𝛿𝑀𝑖 is the first-moment decaying cumulative sum of gradients, 𝛿𝑉𝑖 is the second-moment decaying cumulative sum of gradients, the hat notation 𝛿𝑀, and 𝛿𝑉 are bias-corrected values of 𝛿𝑀 and 𝛿𝑉𝑖 and ŋ is the learning rate.
Non-Convex Optimization in Action
In the context of computational problem formulation, understanding the intuition behind these optimization algorithms will enlighten the learning curve and how deep neural networks learn from complex data. Additionally, understanding the intuition behind these non-convex algorithms will help you to select your optimization algorithm when training machine learning models. In this article, I covered the intuitional point of view for non-convex algorithms and their simple Python implementations. For instance, you’ll have the intuition of why many researchers and data scientists are using Adam optimizers instead of SGD when it comes the training large deep neural networks, as Adam optimizer is adaptive to process and has both first and second-order momentum as opposed to SGD. That’s the end of the article. Let me know if you have issues. Here is how.
Here I am
Twitter | Linkedin | Medium | Mail
References
[1] Wikipedia contributors, ‘Stochastic gradient descent, Wikipedia, The Free Encyclopedia, 6 November 2021, 11:32 UTC, <https://en.wikipedia.org/w/index.php?title=Stochastic_gradient_descent&oldid=1053840730> [accessed 7 November 2021]
Neural Network Optimizers from Scratch in Python was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3bQJFsX
via RiYo Analytics

No comments