https://ift.tt/3FnQZJi How to use concepts from economics, statistics and data science to think more clearly and make better decisions Ph...
How to use concepts from economics, statistics and data science to think more clearly and make better decisions

Concepts help you understand the world. The concepts from data science can be applied throughout life, from finance to healthcare to career choice, forming an important discipline for understanding how the world works. In this article you’ll learn:
- Why the champion team won’t win next season and why early results in science are so often wrong
- How to deal with conflicting information of different strengths
- When you should try something new vs stick with what you already know and like
Now let’s explore how you can use 5 foundational data science concepts to improve your life.
Bayes’ rule
Bayes’ rule is a method for assessing the probabilities of an event. You start with a probability before an event, receive evidence, and update the probability you originally assigned. Bayes’ rule forces us to think probabilistically, and makes us take note of the level of uncertainty we have in our views.
Example
One of the most useful things about Bayes’ rule is that thinking explicitly about the prior probability of an event counteracts our tendency to neglect the base rate. Let’s take a look at an example to illustrate.
Meet Ruby:

Say you notice that Ruby is low energy one day. What’s the probability that she is sick, given this observation? For most people, Ruby being a bit under-the-weather would probably come up in their top explanations for Ruby’s tiredness.
But let’s compute the probability of Ruby being sick using the Bayesian method:
Posterior odds = prior odds ratio x likelihood ratio
Or in diagrams:
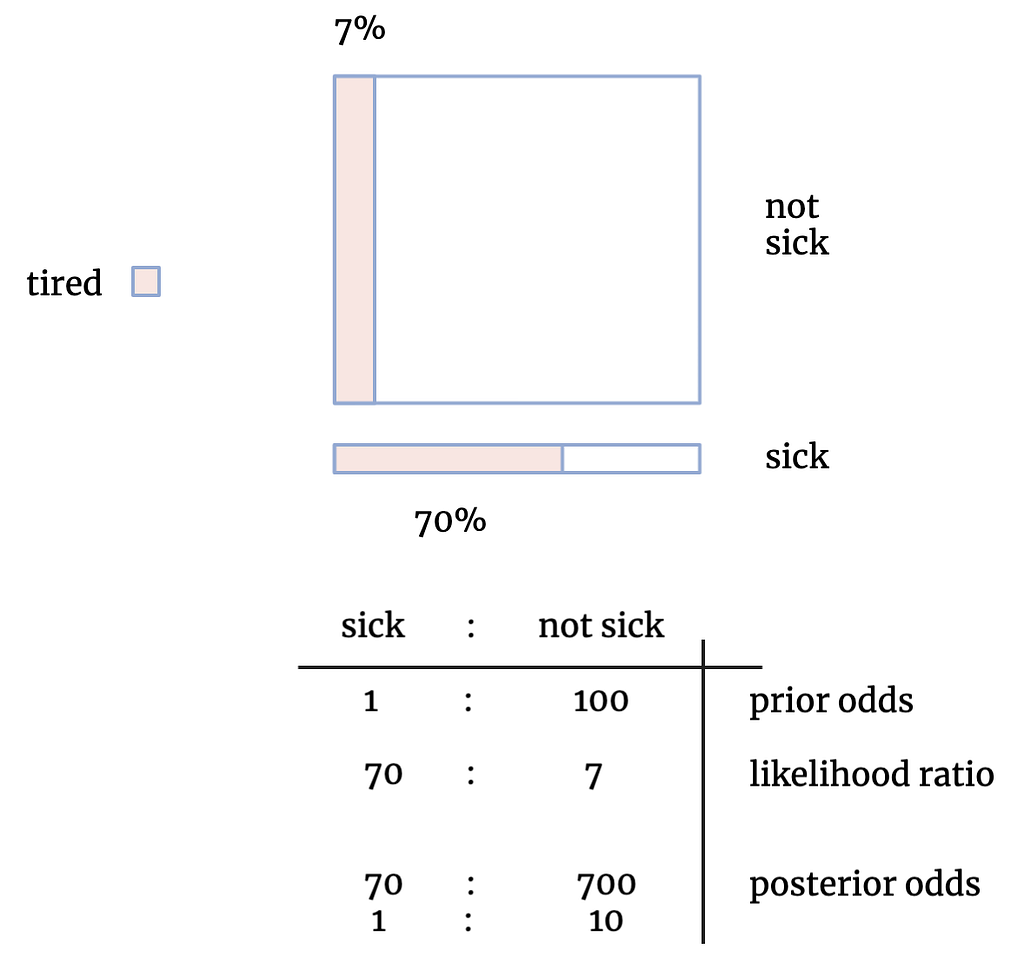
The area of the large square represents the proportion of days throughout the year that Ruby is not sick (i.e. most of them), whereas the small rectangle’s area represents the days that she is sick. That’s the prior odds in the table — Ruby is sick about once every 100 days. The pink colouring within the shapes is the proportion of days where Ruby exhibits tiredness, both for the non-sick days and sick days. We can see that Ruby seems noticeably tired on 7% of her non-sick days, and 70% of her sick days (the likelihood ratio in the table). Finally, the calculation we must do to find out the posterior odds of Ruby being sick given that she seems tired is the product of the prior odds and the likelihood ratio, which cancels down to 1 in 10. So although Ruby seems tired — and tiredness could well be a sign of being ill — it’s still ten times more likely that she’s fine.
Regression to the mean
If your favorite team won the championship last year, what does that mean for their chances of winning next season? To the extent this is due to skill (the team is in good condition, top coach etc.), their win signals that it’s more likely they’ll win next year. But the greater the extent this is due to luck (other teams embroiled in a drug scandal, favourable draw, draft picks turned out well etc.), the less likely it is they’ll win next year.
This is because of the statistical concept of regression to the mean.
Example
If one trial suggests that health chemical YK7483 is outperforming all other treatments for lymphatic filariasis (looking this up is not for the faint-hearted), you shouldn’t put all your faith in that result. When you do a second test of YK7483, it’s more likely to be closer to the mean the second time you test it. If you took the value at face value, and didn’t project for the fact that it will likely regress to the mean, you’d misplace your money. In one systematic study of this effect John Ioannidis analyzed “49 of the most highly regarded research findings in medicine over the previous 13 years” and found 16% of the studies were contradicted, 16% had effects that were smaller in the second study than in the first, 24% remained largely unchallenged and only 44% were replicated. And recall, these are the most highly regarded research findings which you would expect to be more reliable, not just any old sample.
Explore-exploit
The exploration, exploitation trade-off is a dilemma we frequently face in choosing between options. Should you choose what you know and get something close to what you expect (‘exploit’) or choose something you aren’t sure about and possibly learn more (‘explore’)? This happens all the time in everyday life — favourite restaurant, or the new one? Current job, or hunt around? Normal route home, or try another?. You sacrifice one to have the other, so it’s a trade-off. Which of these you should choose depends on how costly the information about the consequences is to gain, how long you’ll be able to take advantage of it, and how large the benefit to you is.
Example
Your small movie production business has had a few hits over the years and you’re trying to work out what your next project should be. You know that if you did a sequel of an old classic it would have mediocre returns. Alternatively, you could try a hot new idea which is highly unpredictable: it could nosedive, meaning you don’t recover what it cost you to make it, or it could be the next Harry Potter series.
Expected Value
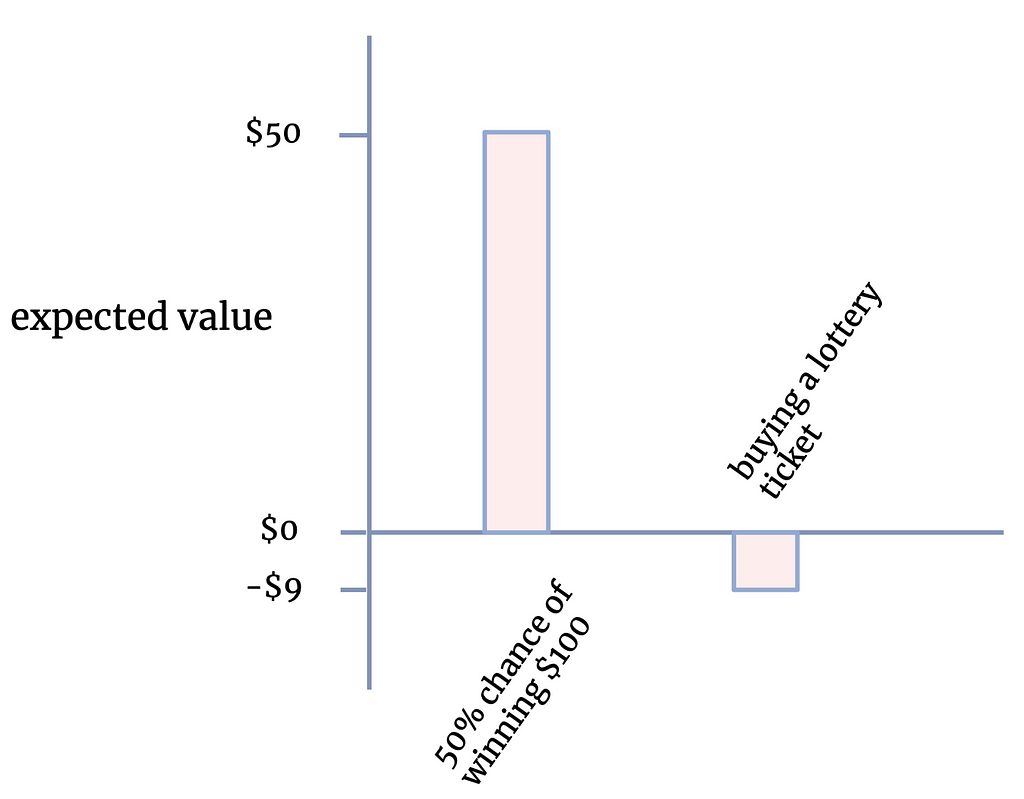
Expected value is the probability of an event happening, multiplied by the value of that event happening. For example, a 50% chance of winning $100 has an expected value to you of $50 (if you don’t mind the risk).
We can use this framework to work out if you should play the lottery. Let’s say a ticket costs $10, and you have a 0.0000001 chance of winning $10 million dollars — should you buy one? Without using expected value, this is a nearly impossible question to evaluate. Multiplied out, the expected value of having one of these tickets is $1 (0.0000001 x $10,000,000 = $1). But it costs you $10 to buy the ticket (1 x $10). So the total expected value of the purchase is negative: $1-$10 = -$9. This is true of most lotteries in real life, hence buying a lottery ticket is just an example of our bias towards excessive optimism.
Example
It turns out that all events have some aspect of risk and value. Insurance companies use this to determine how much to charge you for your premiums. They add up everyone in your reference class, and determine how much it costs them on average in payouts. They then add a little on the top to make a profit, which makes buying insurance net negative (the benefits minus the costs) on expectation, just like buying a lottery ticket. However, this doesn’t mean getting insurance is a bad idea! A lot of people don’t like taking on excessive risk (a small chance of becoming bankrupt feels much worse than paying up for insurance you might never need), so buying insurance is rational. Another way to put this is that we have diminishing marginal returns to extra money (or concave utility functions, for the mathematically inclined).
Pascal’s wager is also an example of using expected value to think about the world. Humans all bet with their lives either that God exists or that he does not. Pascal argues that a rational person should live as though God exists and seek to believe in God. If God does actually exist, such a person will have only a finite loss (some pleasures, luxury, etc.), whereas they stand to receive infinite gains (as represented by eternity in Heaven) and avoid infinite losses (eternity in Hell).
Abstraction
Abstraction is the process of generalising complex events to the concepts that underly them, tucking away the complexities of the situation. The process of abstraction can help us understand the real world by hiding the confusing details, leaving us with general concepts that hold true across domains and can be applied in different situations.
Example
The concept of abstraction is key to making computers work. Computers only understand 1s and 0s, otherwise known as binary or machine code. It would be very time-consuming if a programmer who wanted to programme a computer to play tetris, had to individually write out all the 1s and 0s themselves.
To avoid all that work, programmers develop higher-level languages to control the machine code. Those 1s and 0s are bound up in the syntax of a higher level programming language that is built on top of this machine code. A human programmer can write their software in these easier-to-use languages, and then the computer converts the script into something it understands — the machine code — via an interpreter or compiler. Everybody wins.
Conceptually.org is a free collection of concepts from economics, data science, philosophy, and elsewhere to help you better understand the world. Sign up to learn about 1 concept per week.
5 data science concepts to improve your life was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3FnN8Mo
via RiYo Analytics

No comments