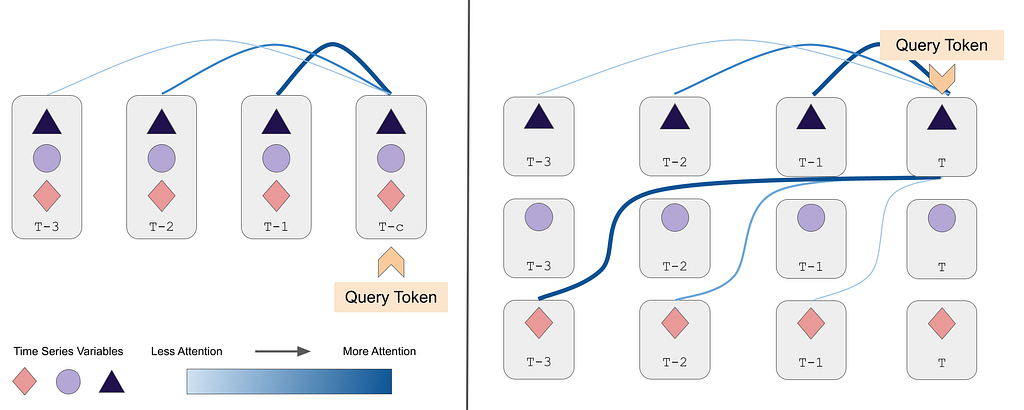
https://ift.tt/3Bn6LSb Spatiotemporal Learning Without a Graph Temporal Self-Attention (left) and Spatiotemporal Self-Attention (right). ...
Spatiotemporal Learning Without a Graph
Many real-world applications of Machine Learning involve making predictions about the outcomes of a group of related variables based on historical context. We might want to forecast the traffic conditions on connected roads, the weather at nearby locations, or the demand for similar products. By modeling multiple time series together, we hope that changes in one variable may reveal key information about the behavior of related variables. Multivariate Time Series Forecasting (TSF) datasets have two axes of difficulty: we need to learn temporal relationships to understand how values change over time and spatial relationships to know how variables impact one another.
Popular statistical approaches to TSF can struggle to interpret long context sequences and scale to complex variable relationships. Deep Learning models overcome these challenges by making use of large datasets to predict rare events far into the future. Many methods focus on learning temporal patterns across long timespans and are based on Recurrent or Convolutional layers. In highly spatial domains, Graph Neural Networks (GNNs) can analyze the relationships amongst variables as a graph of connected nodes. That graph is often pre-defined, e.g., a map of roads and intersections in traffic forecasting.
In this post, we hope to explain our recent work on a hybrid model that learns a graph across both space and time purely from data. We convert multivariate TSF into a super-long sequence prediction problem that is solvable with recent improvements to the Transformer architecture. The approach leads to competitive results in domains ranging from temperature prediction to traffic and energy forecasting.
This is an informal summary of our research paper, “Long-Range Transformers for Dynamic Spatiotemporal Forecasting,” Grigsby, Wang, and Qi, 2021. The paper is available on arXiv, and all the code necessary to replicate the experiments and apply the model to new problems can be found on GitHub.
Transformers and Time Series Forecasting
Transformers are a state-of-the-art solution to Natural Language Processing (NLP) tasks. They are based on the Multihead-Self-Attention (MSA) mechanism, in which each token along the input sequence is compared to every other token in order to gather information and learn dynamic contextual information. The Transformer learns an information-passing graph between its inputs. Because they do not analyze their input sequentially, Transformers largely solve the vanishing gradient problem that hinders Recurrent Neural Networks (RNNs) in long-term prediction. For this reason, Transformers have been applied to datasets with long historical information, including TSF.
Multivariate TSF datasets are usually organized by time: the values of all N variables are represented as a single vector. However, this only allows Transformers to learn relationships between the entire stack of variables across time. In complex Multivariate TSF problems, each variable has meaningful relationships to its history as well as different events in the history of other variables. A standard application of Transformers to TSF data can’t learn this because it treats the values of every variable at a given timestep as a single token in its graph; each variable cannot have its own opinion on the context it should prioritize. This is unlike the NLP tasks where Transformers are so popular, where every token represents a unified idea (a single word).
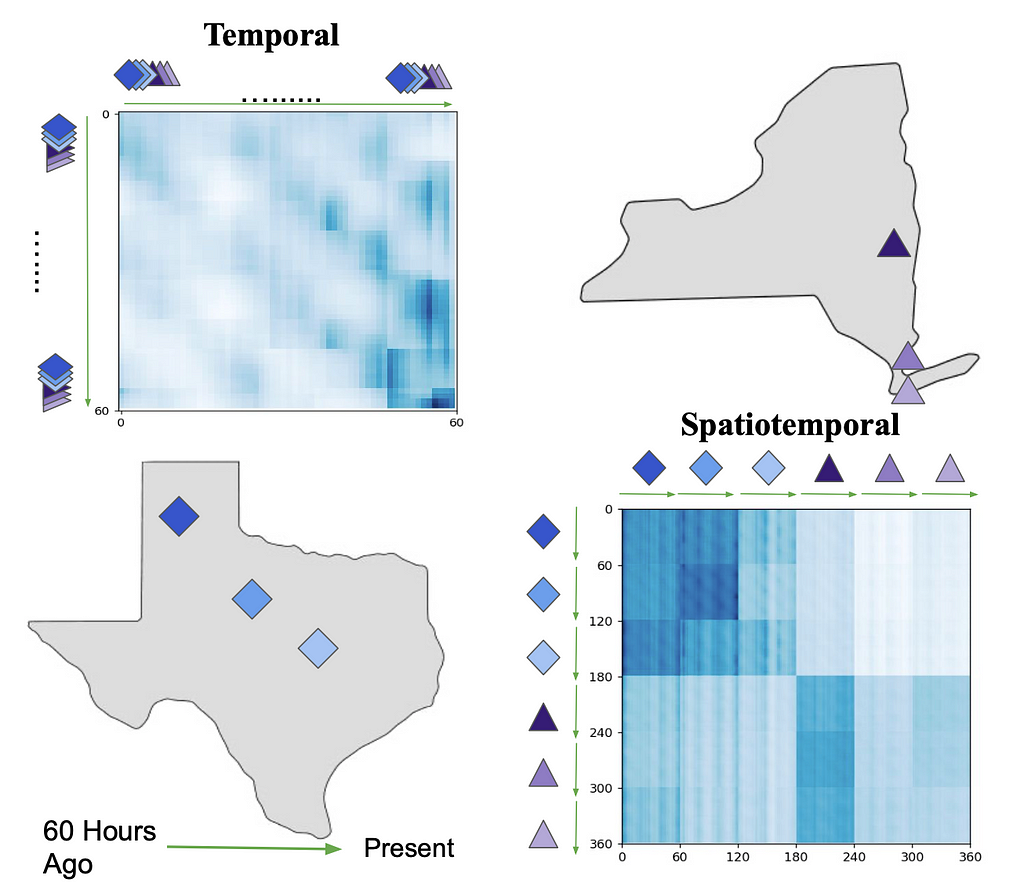
We address this by creating a new prediction problem in which each token represents the value of a single variable per timestep. Transformers are then free to attend to the values of any variable at any time in order to make more accurate predictions. The diagram at the top of this post shows the difference between these two types of attention.
Spacetimeformer
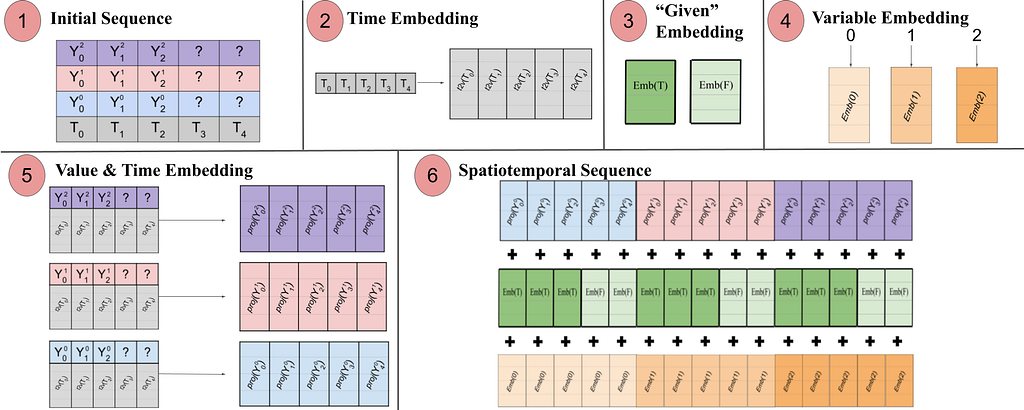
We use an input format in which N variables at T timesteps are flattened into a sequence of (N x T) tokens. The value of each variable is projected to a high-dimensional space with a feed-forward layer. We then add information about the timestep and variable corresponding to each token. The time and variable embeddings are initialized randomly and trained with the rest of the model to improve our representation of temporal and spatial relationships. The values at future timesteps we want to predict are set to zero, and we tell the model which ones are missing with a binary “given” embedding. The different components are summed and laid out such that Transformer MSA constructs a spatiotemporal graph across time and variable space. The embedding pipeline is visualized in the figure below.
Standard Transformers compare each token to every other token to find relevant information in the sequence. This means that the model’s runtime and memory use grows quadratically with the total length of its input. Our method greatly exaggerates this problem by making the sequence N times longer than the timeseries itself. The rest of our approach deals with the engineering challenge of making it possible to train this model without the highest-end GPU/TPUs.
Efficient Transformers are an active area of research in applications with long input sequences. These “Long-Range Transformers” look to fit the gradient computation of longer sequences in GPU memory. They often do this by adding heuristics to make the attention graph sparse, but those assumptions don’t always hold up outside of NLP. We use the Performer attention mechanism, which linearly approximates MSA with a kernel of random features. Performer is efficient enough to fit sequences of thousands of tokens, and lets us train our model in a few hours on one node with 10GB GPUs.
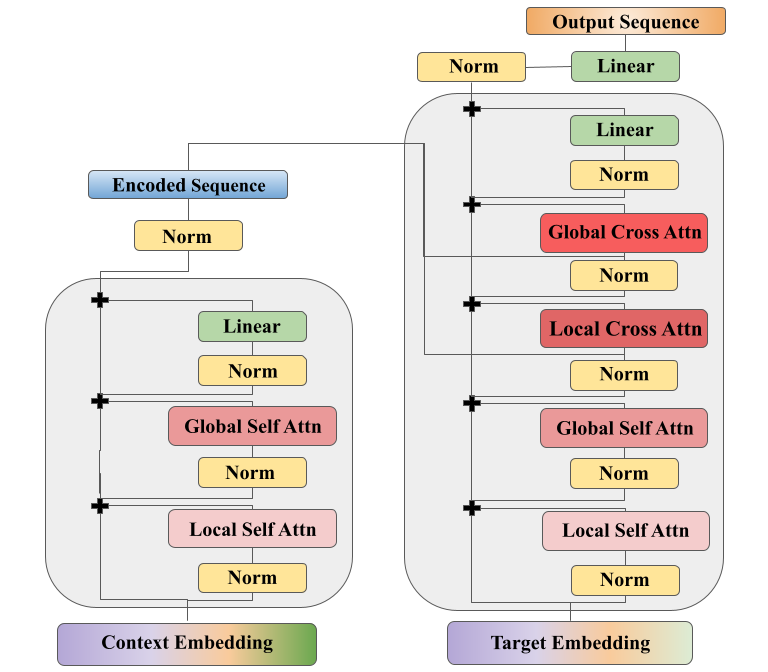
The context sequence of historical data and the target timestamps we’d like to predict are converted to long spatiotemporal sequences. A Performer-based encoder-decoder architecture processes the sequence and predicts the value of each variable at future timesteps as separate tokens. We can then re-stack the predictions to their original format and train to minimize prediction-error metrics like mean squared error. The model can also create a range of forecasts by outputting both the mean and standard deviation of a normal distribution — in which case we train to maximize the probability of the ground-truth sequence. The full model architecture is shown below.
Applications
We compare the model against more standard TSF and GNN methods. Linear AR is a basic linear model trained to make auto-regressive predictions, meaning it outputs one token at a time and recycles its output as an input for the next prediction. LSTM is a standard RNN-based encoder-decoder model without attention. LSTNet is an auto-regressive model based on Conv1D layers and RNNs with skip connections to remember long-term context. DCRNN is a graph-based model that can be used when a pre-defined variable graph is available. Like our method, MTGNN is a TSF/GNN hybrid that learns its graph structure from data but does not use Transformers for temporal forecasting. Finally, we include a version of our own model that does not separate the tokens into a spatiotemporal graph; the values of each variable remain stacked together as usual. This “Temporal” ablation is a stand-in for Informer, but it uses all of the rest of our engineering tricks and training process to isolate the benefits of spatiotemporal attention.
First, we’ll look at a weather forecasting task. We used the ASOS Network to put together a large dataset of temperature readings from airports in Texas and New York. The geographic separation between the two groups makes spatial relationships more important, and those relationships have to be learned from experience because we do not provide any location information. We predict 40, 80, and 160 hours into the future and compare Mean Squared Error (MSE), Mean Absolute Error (MAE) and Root Relative Squared Error (RRSE). This experiment focuses on TSF models because a graph is not available.
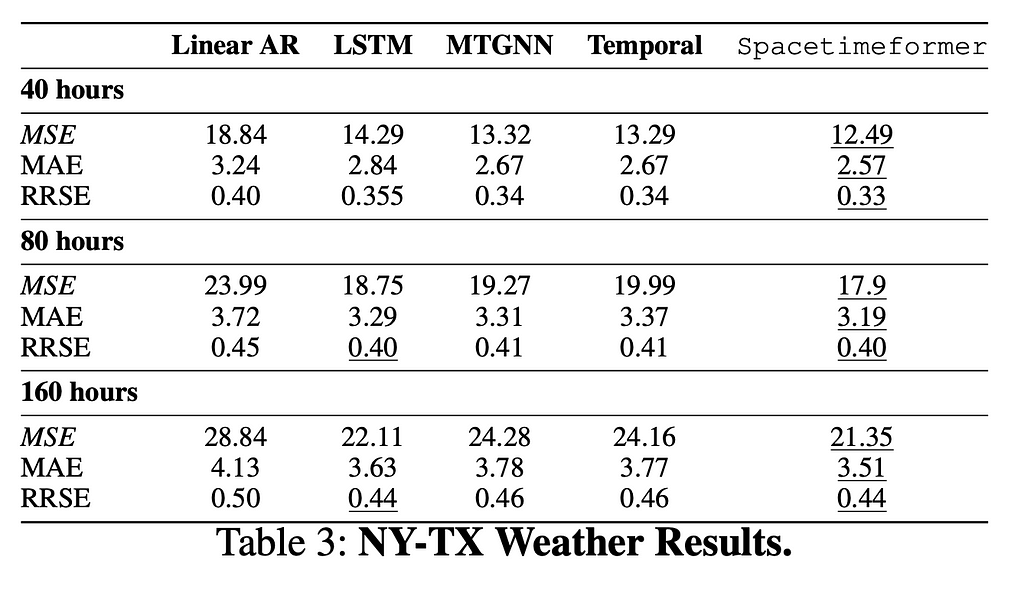
Spacetimeformer outperforms the baselines, and its advantage over the Temporal attention version appears to increase with the length of our predictions. Our goal is to learn a spatiotemporal attention graph, and we can verify that this is what Spacetimeformer accomplishes by visualizing its attention network. Attention matrices visualize MSA by revealing the attention given by each token to the full sequence; each row is one token, and the columns of that row show the token’s attention to the other tokens in the sequence, including itself. The figure below shows the weather station variables and attention matrices of Spacetimeformer and the Temporal-only variant, where darker blue coloring corresponds to more attention. The standard Temporal mechanism learns a sliding wave-like pattern where each token focuses mostly on itself (along the diagonal) and on the very end of the sequence. Spacetimeformer flattens that sequence into separate variables, with each variable having its own sub-sequence of tokens (indicated by a green arrow and the variable shape). This results in a ‘block-structured’ attention matrix where all the tokens of a variable tend to prioritize the timesteps of a subset of the other variables. We can interpret these patterns to understand the spatial relationships the model is learning. In this case, the model can correctly cluster the Texas and New York stations together — and if you zoom in, you can see the same wave-like temporal patterns within each subsequence.
Next, we look at three benchmark datasets in traffic and energy forecasting. AL Solar measures the solar output of 137 sites in Alabama, while the Metr-LA and Pems-Bay datasets measure vehicle speeds at 200+ road sensors around Los Angeles and San Francisco, respectively. We generate 4-hour solar forecasts and 1-hour traffic forecasts. The results are shown in the tables below.

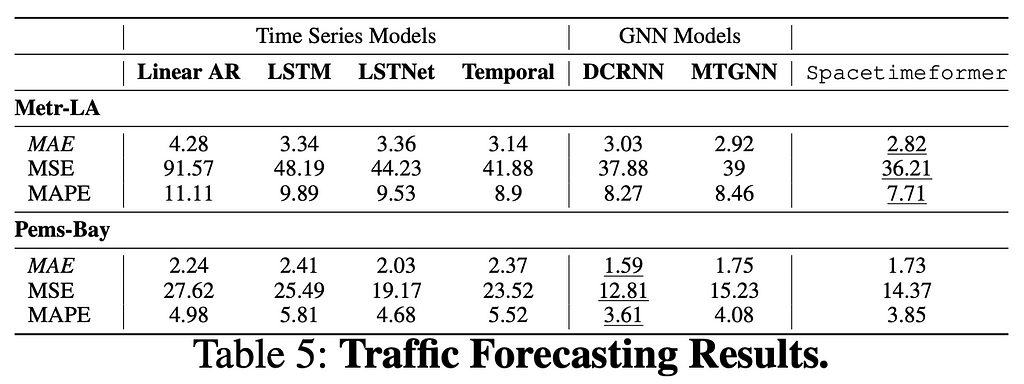
Spacetimeformer learns an accurate prediction model in all cases. The traffic results are interesting because the complex road network makes these problems a common benchmark in Graph Neural Network research, where the map can be turned into a graph and provided to the model in advance. Our model has comparable predictive power while implicitly learning a roadmap from data.
If you’d like to apply this method to new problems, the source code for the model and training process is released on GitHub at QData/spacetimeformer. A more detailed explanation with additional background and related work can be found in our paper.
— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — —
Written by Jake Grigsby, Zhe Wang, and Yanjun Qi. This research was done by the QData Lab at the University of Virginia.
Multivariate Time Series Forecasting with Transformers was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3jLKAz9
via RiYo Analytics

No comments