https://ift.tt/nL2T8VN A brief look at the science of revenue management with a Python demonstration Photo by Evelyn Paris on Unsplash ...
A brief look at the science of revenue management with a Python demonstration

If you’ve ever bought plane tickets, you are certainly aware of the impact timing has on the price. A leisure flyer who buys their ticket six months in advance may only pay $200 for their seat, while the businessman who buys the day before pays $3,300 for the seat right next to them. We encounter similar situations whenever we book a hotel room, rent a car, or schedule tee time at a golf course. If you have ever wondered what is behind this and how it works, the answer is Revenue Management.
Revenue Management is a data science-driven enterprise that brings together customer segmentation, predictive analytics & machine learning, design of experiments, and mathematical optimization in an orchestrated manner to maximize revenues attained with existing capacity. By understanding the principles of Revenue Management, data scientists can apply their skills to help their firms and clients see substantial increases in revenue.
The Science of Revenue Management
Revenue Management (RM) is the science of predicting real-time customer demand at the micro-market level and optimizing the price and availability of products or services [1]. RM was pioneered by American Airlines in the 1980’s in response to a threat posed by a new low-fare competitor, People Express. American’s RM system differentiated prices between leisure and business flyers. It also used optimization algorithms to determine how many seats to open to early-booking, low-fare flyers and how many to protect for later-booking, high-fare business flyers. This approach proved highly successful, restoring American’s profitability while ultimately leading to the closure of People Express. As a result, many other industries have likewise begun employing RM.
The goal of RM is to offer the right product or service to the right customer at the right time through the right channel at the right price. Traditionally, RM was developed for businesses operating under a few conditions:
- Fixed Capacity: Airlines have a fixed fleet size, and hotels have a fixed number of rooms, for example.
- Perishable Products or Services: Unsold seats on a flight or hotel rooms on a given date cannot be sold later, for example.
- Customers Reserve Resources Ahead of Time (e.g., booking a flight or hotel room)
Today, RM techniques are being adapted beyond these assumptions for new industries such as E-commerce. In general, however, RM involves four interrelated activities:

1. Segment the Market
The first activity involves identifying different customer segments based on usage patterns or desires. For example, airlines segment customers into leisure flyers who book early and business flyers who book later, while car rental companies segment customers based on whether they want compact, mid-sized, or deluxe vehicles.
2. Determine the Price Response
After segmenting, we must determine the price response and choose the best prices accordingly. If we price a segment’s offering too low, we may have no trouble selling, but we will also leave revenue on the table. By contrast, if we price too high we risk losing revenue through customers balking at our offers. We must therefore determine the best price each segment is willing to pay and the impact price increases will have on demand. This is often done through pricing experiments and can also incorporate competitor and industry data. Experiments should be conducted in real market conditions and repeated periodically, as factors including inflation, wage growth, holidays, and new competitors can all impact the price response.
3. Forecast Demand
To begin applying RM, we need to specify a time horizon and then forecast demand for each segment in each usage slot within the horizon. As RM works at the micro-economic level, the time horizon is typically near-term and short in duration. A usage slot might be a flight leg in the airline industry, or a Friday-Sunday stay in the hospitality industry. So, for example, we forecast the demand for leisure and business flyers on each flight leg, or the demand for small and large hotel rooms for each bookable time interval.
4. Optimize Capacity Allocation
Once we estimate the demands for each segment, we need to determine how to allocate our capacity to maximize revenue over the horizon. This tells us, for example, how many seats to sell to leisure flyers and how many to hold for business flyers, or how many cars to use to meet compact demand and how many to use for deluxe demand in each time slot. This can be mind-bogglingly difficult to do by hand because usage slots can overlap and prevent the same resources from being used for both. Substitutions can also be done when advantageous (for example, offering a large hotel room to someone who requests a small room), further increasing the complexity. For this reason, capacity allocation is typically accomplished via integer programming.
These four activities should be thought of as key ingredients rather than strict steps in a process. Some RM systems focus primarily on capacity allocation, fixing prices ahead of the sale period, while others update prices frequently in response to ever-changing market conditions. These activities need to be coordinated in a tailored way for each individual application to achieve the best return on investment.
An Example Scenario: Optimizing Vacation Cabin Rental Revenue
We will illustrate one RM activity, capacity allocation, and demonstrate the impact it can have on revenues. This example can be viewed in a Jupyter notebook here. Source code and data files for this example can be found here.
A vacation cabin rental company owns the following resources:
- 3 small cabins
- 5 medium cabins
- 3 large cabins
We will assume that we have already determined the best prices and an accurate demand forecast for an upcoming long weekend as shown below:

The goal is to determine how many of each cabin type to allocate to the different demand slots to maximize revenues. We begin by importing the key libraries and reading in our data:
Modeling the Problem
We will formulate and solve an integer programming (IP) model to allocate capacity to the demand forecast in a way that maximizes the revenue attained. This model assigns cabins to demand slots in the form of (time interval, cabin size) pairs and employs binary indicators to enable specification of allowable substitutions. We begin by defining the model inputs:

Next, we define our decision variables:
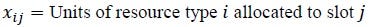
The optimization model can now be formulated as follows:
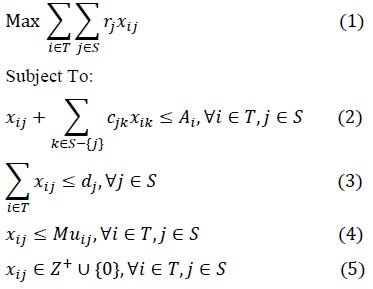
In the model above, the objective function (1) is simply the sum of all revenue attained over the period. Constraints in (2) ensure that we never overbook the available capacity for any cabin type. We do this by ensuring that for any cabin type i and slot j , the total number of type i cabins assigned either to slot j or any other slot that overlaps j’s start time does not exceed the number of type i cabins available. Constraints in (3) ensure we don’t allocate more cabins than demand for any slot. Constraints in (4) ensure that we never make invalid substitutions by assigning cabins to slots they cannot satisfy. Finally, constraints in (5) ensure non-negative integer domains for the decision variables.
Below we define a Python function to construct an instance of this IP model from the input data:
Obtaining an Optimal Capacity Allocation Plan
Now we will create an optimize function to solve the model, which will determine our optimal sales plan and revenue attained. To accomplish this, we first need to create a few helper functions to transform our raw data into the format needed by the model.
Now we can optimize and view the revenues with the resulting sales plan. In this example, we will allow larger cabins to substitute for smaller ones.
Running the code above gives the following:
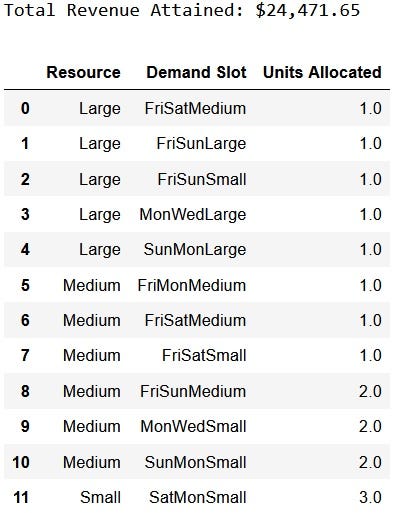
Interestingly, as we look at this optimal allocation plan, we note the many instances of substituting larger cabins for smaller ones that occur. As we will see, allowing these kinds of substitutions can have a big impact on revenues.
Solving the Human Way: First Come, First Served
It is instructive to compare the optimal policy to one a human might implement without RM. Under such circumstances, rather than allocating to a demand forecast, an agent would simply sell cabin bookings as the requests come in a first-come-first-served (FCFS) order. It would not make a lot of sense to use substitutions in this case either, since we never know if the next request will be for a larger cabin which brings in more revenue.
The revenue generated by FCFS is very sensitive to the order in which requests come; these may come in an order that happens to tie up our cabins in a very sub-optimal way, or we may get lucky and get an ordering that generates near-maximal revenues. The code below implements the FCFS policy along with a pre-processing function to transform the raw data into the form needed by the algorithm. In the pre-processing function, we randomly order the booking requests to simulate the way they would come in the real world.
Comparing Policies
Below we will compare two variations of optimization (one with no substitutions, and one that allows larger cabins to sub for smaller ones) against FCFS to see the impact on revenues. We will run FCFS 100 times, randomly ordering the booking requests each time, and compare the worst, median (i.e. typical), and best cases to the two optimization results.
Running this gives the following results:
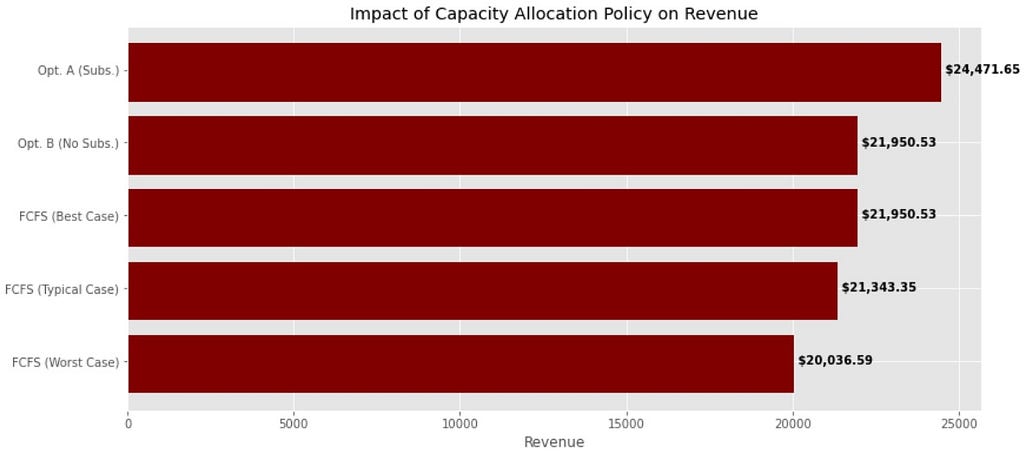
Comparing policies, we see that FCFS will typically leave revenue on the table — and if we get unlucky, this can be a significant amount. Only in the best case will FCFS reach the maximum revenue possible under the assumption of no substitutions allowed (which is always reached by the Optimization B policy). By allowing substitutions and optimizing, however, we attain a big boost in revenues — amounting to an increase of more than 22% over the worst-case (or well over $4,000) for the weekend. Moreover, this extra revenue is earned using existing capacity without incurring any additional costs, so it is entirely profit. This comparison demonstrates the impact RM can make.
As a final caveat, we point out that effective capacity allocation relies on good demand forecasts to use as optimization inputs. Some weeks our forecast will miss the mark. However, assuming forecasts can be typically made with reasonable accuracy, systems that use RM will in the aggregate outperform those that don’t.
Conclusion
Revenue Management is a science that can significantly increase revenues attained with existing capacity. By incorporating the elements of RM into the sales process, companies can begin to increase revenues without incurring additional operational costs.
References
[1] Cross, R.B. (1997). Revenue management: hard-core tactics for market domination. New York: Broadway Books, p. 276.
Optimizing Vacation Cabin Rental Revenues was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium
https://towardsdatascience.com/optimizing-vacation-cabin-rental-revenues-730d2847a2ed?source=rss----7f60cf5620c9---4
via RiYo Analytics

No comments