https://ift.tt/KgIRUX7 Compute (in SQL) the minimum number of meeting rooms needed to schedule a set of meetings Photo by Dane Deaner on...
Compute (in SQL) the minimum number of meeting rooms needed to schedule a set of meetings

The meeting room problem asks you to determine the least number of meeting rooms needed to be able to schedule all the meetings from a given set such that there are no conflicts. We shall see how to solve this in declarative SQL alone.
Previous Article: Validate Balanced Parenthesis using SQL
Problem Statement
Given a set of meeting start and end times (both inclusive), determine the least number of meeting rooms needed to schedule all the meetings without any conflicts (i.e. there should be no situation where a meeting room is not available for a meeting, and neither should 2 meetings be scheduled at overlapping times in a give meeting room).
Online Coverage
This problem is pretty popular in programming circles, and you can find coverage here:
In fact, there are discussions about solving this problem in SQL too (this is generally rare for the types of problems I’ve been covering in my articles).
- A Cool SQL Problem (And Why It Is Also a Bullshit SQL Problem)
- (Stack Overflow) Minimum number of Meeting Rooms required to Accommodate all Meetings in MySQL
Input Table Schema
The input table looks like this:
CREATE TABLE meetings(
idx SERIAL PRIMARY KEY,
start_at TIMESTAMP NOT NULL,
end_at TIMESTAMP NOT NULL
);
The columns have the following meaning:
- idx: The index (unique ID) of this meeting
- start_at: The timestamp at which this meeting starts
- end_at: The timestamp at which this meeting ends (the meeting is considered to include this timestamp, so a meeting that begins at this timestamp can not be scheduled in the same room as this meeting).
INSERT INTO meetings(start_at, end_at) VALUES
-- { 1, 18 }, { 18, 23 }, { 15, 29 }, {4, 15}, {2, 11}, {5, 13}
('01/01/2022', '01/18/2022'),
('01/18/2022', '01/23/2022'),
('01/15/2022', '01/29/2022'),
('01/04/2022', '01/15/2022'),
('01/02/2022', '01/11/2022'),
('01/05/2022', '01/13/2022');
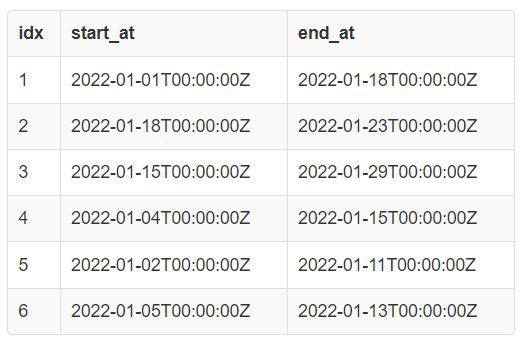
SELECT * FROM meetings;
First solution: O(n²)
This solution is discussed in both the online articles (links above) that talk about solving this problem using SQL.
The main idea is that one should look at every point in time (every second for example) between the first and last timestamp at which meetings are scheduled and check how many meetings overlap with that timestamp.
An optimization that can be performed is that instead of checking every point in time, we only check the “interesting” points in time — i.e. the ones where a meeting either begins or ends. This is because between any 2 such “interesting” points, there will be no change in the number of scheduled meetings.
This solution has a runtime complexity of O(n²) since we need to join every meeting O(n) and match it up with every unique time point O(n) that corresponds to the start or end time point of a meeting.
WITH unique_time_points AS (
SELECT ts
FROM (
SELECT start_at AS ts
FROM meetings
UNION
SELECT end_at AS ts
FROM meetings
) AS start_and_end_ts
),
joined AS (
SELECT
lhs.ts, COUNT(rhs.idx) AS num_overlaps
FROM unique_time_points lhs INNER JOIN meetings rhs
-- Join condition checks how many scheduled meetings intersect
-- the point "ts".
ON lhs.ts BETWEEN rhs.start_at AND rhs.end_at
GROUP BY lhs.ts
ORDER BY lhs.ts ASC
)
SELECT * FROM joined;
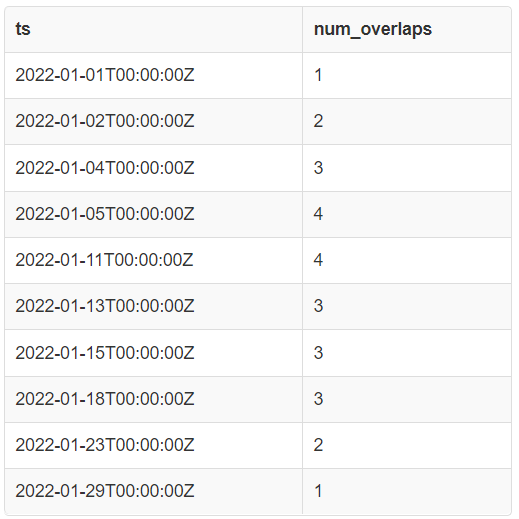
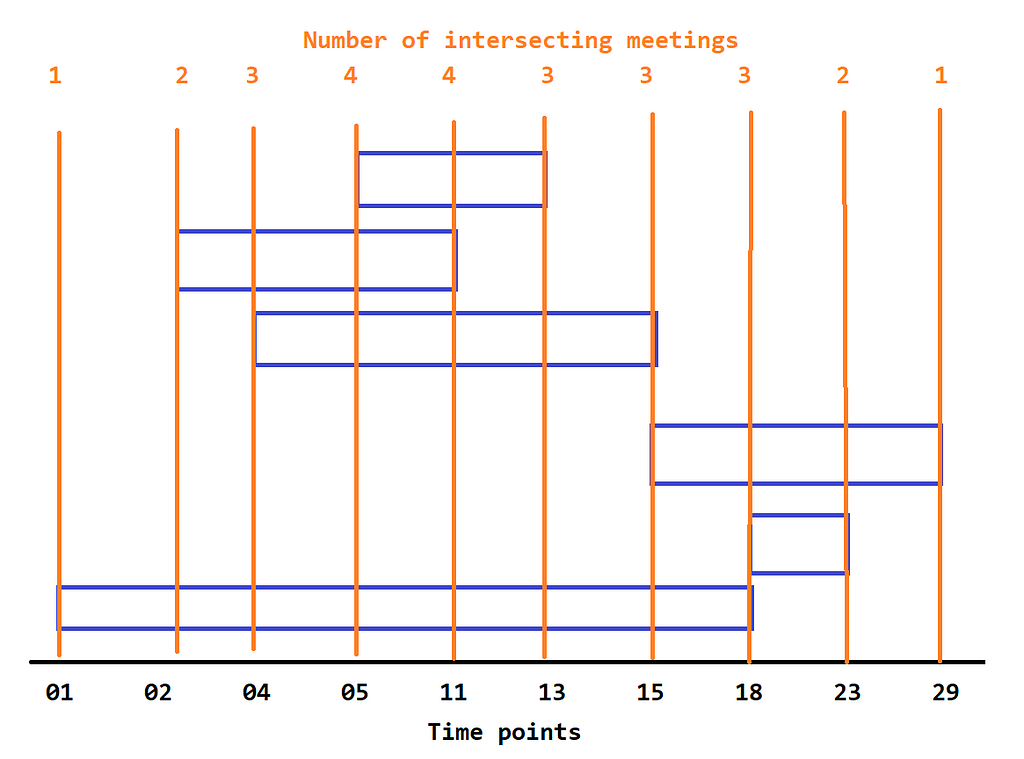
Here, we can see that the minimum number of meeting rooms we need to schedule all the meetings is 4. This happens between time points 2022–01–05 and 2022–01–11.
This is what the above output looks like graphically.
Estimated Cost: The estimated cost for this query on a table of 6 rows is 104k.
Second solution: O(n log n)
The main idea behind this solution is that once you have all the unique time points at which meetings start and end, one can simply track how many “running” meetings are present at those time points.
Counter: When a start time point is encountered, we need to increment a single counter (running_sum), and when a meeting end time point is encountered, we need to decrement this same counter.
Counting overlaps: In case of meetings both starting and ending at a specific time point, we need to be careful to first increment the counter and then decrement it since the meeting is considered to be fully occupying its end time point. Hence, we have code that says: ORDER BY ts ASC, delta DESC — i.e. if we don’t order by delta descending, then we could process the end time point before the start time point, and that would undercount the number of overlapping meetings.
The runtime complexity of this solution is O(n log n) since it’s dominated by the cost of ordering all the unique time points in non-decreasing order of timestamp.
WITH unique_time_points AS (
SELECT start_at AS ts, +1 AS delta
FROM meetings
UNION
SELECT end_at AS ts, -1 AS delta
FROM meetings
),
with_running_sum AS (
SELECT
ts,
delta,
-- We need to process time points in "ts" order. Also in case
-- there are multiple time points, we need to first process a
-- meeting start and then a meeting end since a meeting end is
-- assumed to occupy its end timepoint. This ensures that we
-- don't under-count the number of simultaneously scheduled
-- meetings.
SUM(delta) OVER (ORDER BY ts ASC, delta DESC) AS running_sum
FROM unique_time_points
)
SELECT * FROM with_running_sum;
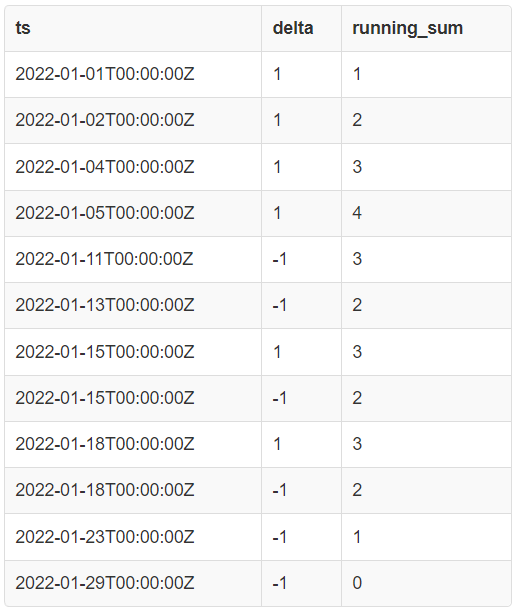
We can see that the minimum number of meeting rooms (4) needed to schedule all meetings without conflict is between 2022–01–05 and 2022–01–11 (same as the solution above).
This is what the output above looks like graphically.
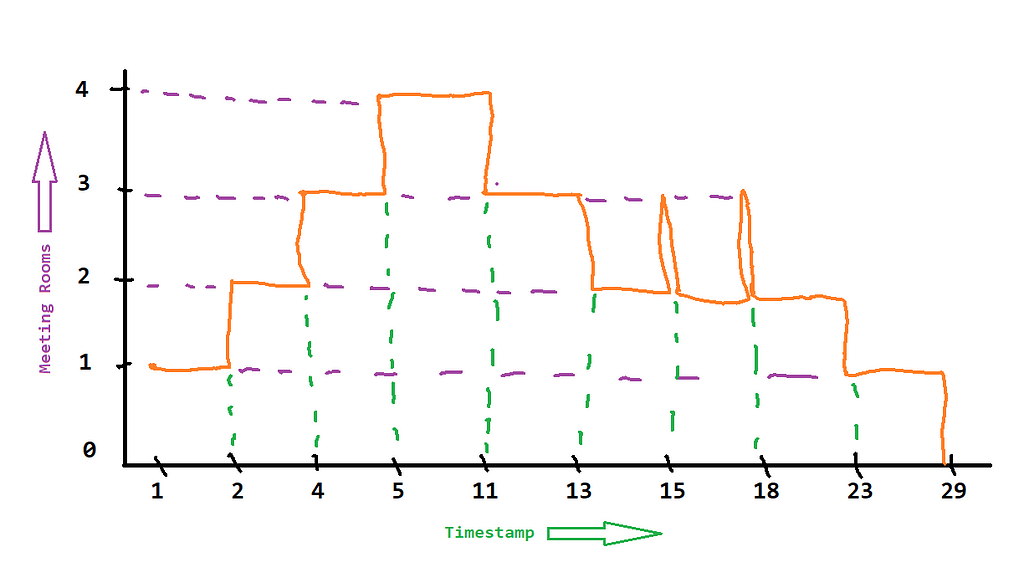
Estimated Cost: The estimated cost for this query on a table of 6 rows is 474.
SQL Fiddle
The SQL Fiddle link to all the solutions in this post can be found here.
Conclusion
This problem has some similarities with the previous problem we saw (Validate Balanced Parenthesis using SQL) in so far as the use of the running sum using SQL window functions is concerned.
We saw how we can use SQL window functions (yet again) to see how one can leverage a simple concept such as a running sum to solve seemingly complex problems.
Minimum Meeting Rooms Problem in SQL was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium
https://towardsdatascience.com/minimum-meeting-rooms-problem-in-sql-4d3a92365bdf?source=rss----7f60cf5620c9---4
via RiYo Analytics

No comments