https://ift.tt/WUKtGgx How to implement a solution in a declarative query language The Maximum Sum Subarray Sum problem asks you to find t...
How to implement a solution in a declarative query language
The Maximum Sum Subarray Sum problem asks you to find that subarray of an array of integers that has the greatest sum of elements. It is a popular computer science programming problem usually solved in imperative programming languages such as C++, Java, Python, etc… However, it’s interesting to look at how it can be implement in a declarative query language such as SQL.

I hope to make this the first in a series of many posts that try to solve traditional programming problems using declarative SQL syntax. Why? Because it’s fun!
Problem Statement
Given an array of integers, find the contiguous sub-array of integers (with at least 1 element from the original array) that has the maximum sum of elements.
This problem’s discussion can be found at numerous places including:
All the links above discuss an O(n) time implementation in a conventional programming language. However, we look at building an O(n) time solution entirely in SQL (without any of the procedural extensions).
Input Table Schema
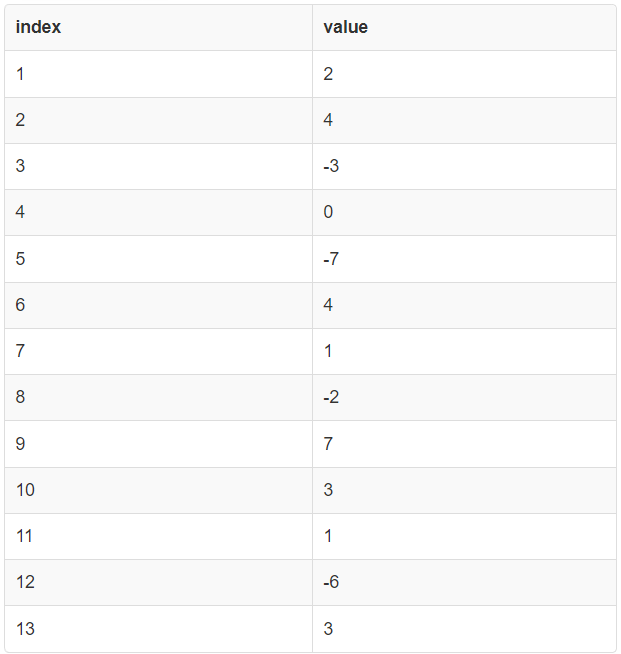
CREATE TABLE array_data(index SERIAL PRIMARY KEY, value INTEGER NOT NULL);
INSERT INTO array_data(value)
VALUES(2), (4), (-3), (0), (-7), (4), (1), (-2), (7), (3), (1), (-6), (3);
SELECT * FROM array_data;
First Solution: O(n³)
The obvious first solution is to generate every pair of valid indexes that a subarray can have (which is O(n²) since every index is paired with an index after it) and then for each such pair, compute the sum of values within that range.
Computing the sum takes linear time over the input (which is every pair of indices), and hence the overall cost of this solution is O(n³)
WITH all_pair_sums AS (
SELECT
lhs.index AS begin_idx,
rhs.index AS end_idx,
SUM(for_values.value) AS array_sum
FROM
array_data lhs INNER JOIN array_data rhs
ON lhs.index <= rhs.index
INNER JOIN array_data for_values
ON for_values.index BETWEEN lhs.index AND rhs.index
GROUP BY 1, 2
ORDER BY lhs.index ASC, rhs.index ASC
)
SELECT * FROM all_pair_sums
WHERE array_sum = (SELECT MAX(array_sum) FROM all_pair_sums);

Estimated Cost: The estimated cost (according to EXPLAIN) for this query on an input table with 13 rows is 108M.
Second Solution: O(n²)
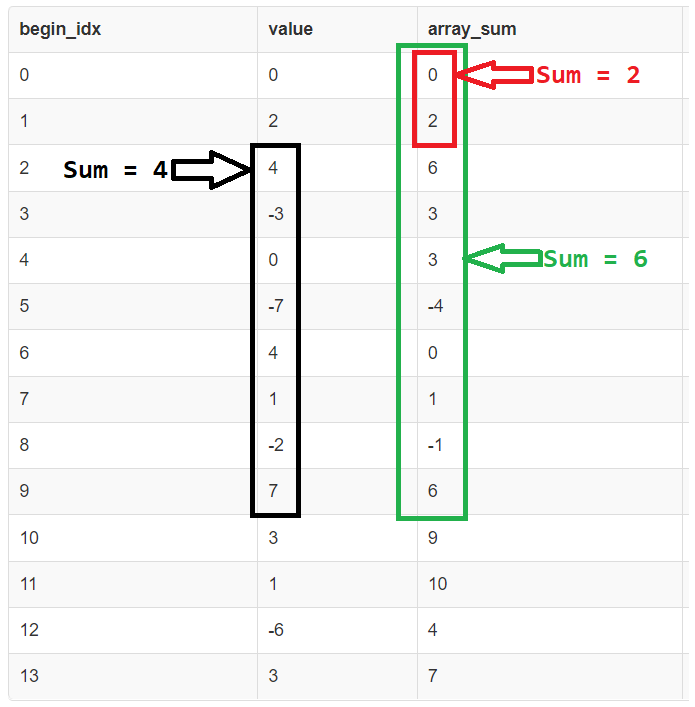
The first optimization we can perform is avoid repeatedly computing the of every array starting at a given array index (begin_idx). Instead, we can maintain a running-sum for every subarray that starts at a given index.
This requires the use of Window Functions, and reduces the cost to O(n²), since we are processing every index for every array index before it.
WITH all_pair_sums AS (
SELECT
lhs.index AS begin_idx,
rhs.index AS end_idx,
SUM(rhs.value) OVER (PARTITION BY lhs.index ORDER BY rhs.index ASC) AS array_sum
FROM
array_data lhs INNER JOIN array_data rhs
ON lhs.index <= rhs.index
ORDER BY lhs.index ASC, rhs.index ASC
),
with_max AS (
SELECT
begin_idx,
end_idx,
array_sum,
MAX(array_sum) OVER() AS max_subarray_sum
FROM all_pair_sums
)
SELECT begin_idx, end_idx, array_sum
FROM with_max
WHERE array_sum = max_subarray_sum;
Here, the array_sum column stroes the running sum of an array starting at index begin_idx and ending at end_idx.

Estimated Cost: The estimated cost (according to EXPLAIN) for this query on an input table with 13 rows is 371k. That’s a 99.65% reduction compared to the previous approach.
Third Solution: O(n)
Observation: To find the sum of a subarray starting at index i and ending at index j, we can find the sum of the subarray [0..j] and from it subtract the value of the sum of the subarray [0..i-1]. In other words, sum[i..j] = sum[0..j] — sum[0..i-1].
The column array_sum above stores the value of the sum of elements of the subarray [0..begin_idx].
The final code for this solution is shown below.
WITH running_sum AS (
SELECT
index AS begin_idx,
value,
SUM(value) OVER (ORDER BY index ASC) AS array_sum
FROM
(SELECT 0 AS index, 0 AS value
UNION ALL
SELECT * FROM array_data
) AS temp
ORDER BY index ASC
),
running_sum_with_min AS (
SELECT
begin_idx,
value,
array_sum,
MIN(array_sum) OVER(ORDER BY begin_idx ASC) AS min_sum_so_far
FROM running_sum
),
sum_of_subarray AS (
SELECT
begin_idx,
value,
array_sum,
min_sum_so_far,
array_sum - LAG(min_sum_so_far, 1) OVER(ORDER BY begin_idx ASC) AS subarray_sum
FROM running_sum_with_min
),
max_sum_of_subarray AS (
SELECT
begin_idx,
value,
array_sum,
min_sum_so_far,
subarray_sum,
MAX(subarray_sum) OVER() AS max_subarray_sum
FROM sum_of_subarray
)
SELECT *
FROM max_sum_of_subarray
WHERE subarray_sum = max_subarray_sum;
If you print the intermediate table max_sum_of_subarray, this is what it looks like. The row highlighted in red is the one that holds the value of the contiguous subarray with the largest sum.
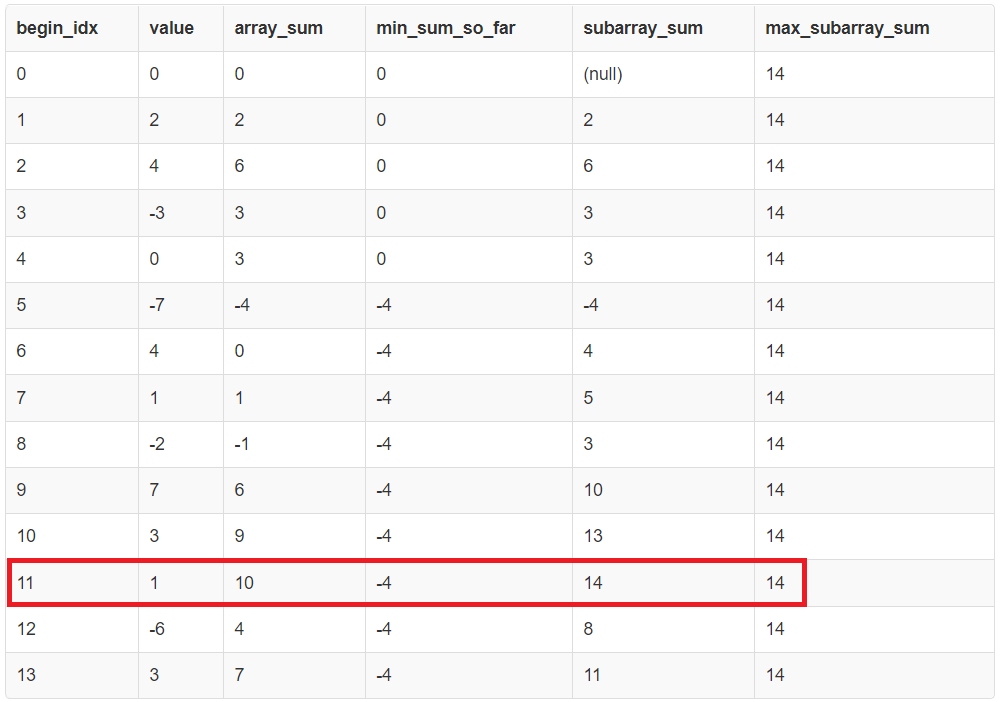
One drawback of this solution is that while we have the end index, we don’t have the start index. This can be trivially fetched by running another query on the intermediate table to search for the first occurrence of the value -4.
This subarray is the one between indexes [6..11]. The value of the sum of elements in this subarray is 10 — (-4) =14.
Note that we insert a dummy row with (index, value) = (0, 0) to ensure that the LAG operation for the first valid row (i.e. row with index = 1) doesn’t end up generating a NULL value, and hence resulting in an incorrect result.
Estimated Cost: The estimated cost (according to EXPLAIN) for this query on an input table with 13 rows is 695. That’s a 99.99% reduction compared to the first approach, and a 99.81% reduction compared to the 2nd approach.
Why is this solution said to be O(n) even though there’s an ORDER BY clause in multiple CTEs in the SQL for this solution?
The original input table’s index column is a primary key column (hence unique). PostgreSQL’s default index type is B-Tree, allows doing a sorted full table scan, which is what we are basically doing in all the CTEs in this solution. Hence, we expect that the optimizer will notice this (coupled with the fact that intermediate tables also come out sorted) and avoid the sort operation entirely. Even if it is unable to deduce this, the running time regresses to O(n log n), but not worse than that.
SQL Fiddle
The SQL Fiddle link to all the solutions in this post can be found here.
Conclusion
We saw numerous ways of solving the same problem in SQL, with varying levels of efficiency. Even though the last solution has the most amount of code, it’s the most efficient in terms of running time and CPU utilization. Breaking down the solutions into smaller CTEs helps code readability and maintainability.
If you’d like to see more conventional programming problems solved using declarative SQL syntax, please add a comment and I’ll try to get to it if possible or write why it may be hard to do.
Maximum Subarray Sum Using SQL was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium
https://towardsdatascience.com/maximum-subarray-sum-using-sql-e1befa75d055?source=rss----7f60cf5620c9---4
via RiYo Analytics

ليست هناك تعليقات