https://ift.tt/u19pfkb A brief guide on multicollinearity and how it affects multiple regression models. Photo by kylie De Guia on Unsp...
A brief guide on multicollinearity and how it affects multiple regression models.

You may have vague recollections from your university statistics courses that multicollinearity is a problem for multiple regression models. But just how problematic is multicollinearity? Well, like many topics in statistics, the answer isn’t entirely straightforward and depends on what you’re wanting to do with your model.
In this post, I’ll step through some of the challenges that multicollinearity presents in multiple regression models, and provide some intuition for why it can be problematic.
Collinearity and Multicollinearity
Before moving on, it’s a good idea to first nail down what collinearity and multicollinearity are. Luckily, if you’re familiar with regression the concepts are quite straightforward.
Collinearity exists if there is a linear association between two explanatory variables. What this implies is, for all observations i, the following holds true:
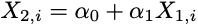
Multicollinearity is an extension of this idea and exists if there are linear associations between more than two explanatory variables. For example, you might have a situation where one variable is linearly associated with two other variables in your design matrix, like so:
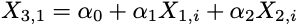
Strictly speaking, multicollinearity is not correlation: rather, it implies the presence of linear dependencies between several explanatory variables. This is a nuanced point — but an important one — and what both examples illustrate is a deterministic association between predictors. This means there are simple transforms that can be applied to one variable to compute the exact value for another. If this is possible, then we say we have perfect collinearity or perfect multicollinearity.
When fitting multiple regression models, it is exactly this that we need to avoid. Specifically, a critical assumption for multiple regression is that there is no perfect multicollinearity. So, we now know what perfect multicollinearity is, but why is it a problem?
Breaking Ranks
In a nutshell, the problem is redundancy because perfectly multicollinear variables provide the same information.
For example, consider the dummy variable trap. Suppose we are provided with a design matrix that includes two dummy coded {0, 1} columns. In the first column rows corresponding with “yes” responses are given a value of one. In the second column, however, rows that have “no” responses are assigned a value of one. In this example, the “no” column is completely redundant because it can be computed from the “yes” column ( “No” = 1 — “Yes”). Therefore, we don’t require a separate column to encode “no” responses because the zeroes in the “yes” column provide the same information.
Let’s extend this idea of redundancy a little further by considering the matrix below:
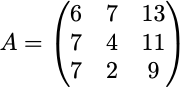
Here, the first two columns are linearly independent; however, the third is actually a linear combination of columns one and two (the third column is the sum of the first two). What this means is, if columns one and three, or columns two and three, are known, the remaining column can always be computed. The upshot here is that, at most, there can only be two columns that make genuinely independent contributions — the third will always be redundant.
The downstream effect of redundancy is that it makes the estimation of model parameters impossible. Before explaining why it’ll be useful to quickly define the moments matrix:
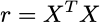
Critically, to derive the ordinary least squares (OLS) estimators r must be invertible, which means the matrix must have full rank. If the matrix is rank deficient then the OLS estimator does not exist because the matrix cannot be inverted.
Okay, so what does this all mean?
Without going into too much detail, the rank of a matrix is the dimension of the vector space spanned by its columns. The simplest way to parse this definition is as follows: if your design matrix contains k independent explanatory variables, then rank(r) should equal k. The effect of perfect multicollinearity is to reduce the rank of r to some value less than the maximum number of columns in the design matrix. The matrix A above, then, only has a rank of 2 and is rank deficient.
Intuitively, if you’re throwing k pieces of information into the model, you ideally want each to make a useful contribution. Each variable should carry its own weight. If you instead have a variable that is completely dependent on another then it won’t be contributing anything useful, which will cause r to become degenerate.
Imperfect Associations
Up until this point, we have been discussing the worst-case scenario where variables are perfectly multicollinear. In the real world, however, it’s pretty rare that you’ll encounter this problem. More realistically you’ll encounter situations where there are approximate linear associations between two or more variables. In this case, the linear association is not deterministic, but instead stochastic. This can be described by rewriting the equation above and introducing an error term:
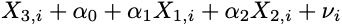
This situation is more manageable and doesn’t necessarily result in the degeneracy of r. But, if the error term is small, the associations between variables may be nearly perfectly multicollinear. In this case, though it’s true that rank(r) = k, model fitting may become computationally unstable and produce coefficients that behave quite erratically. For example, fairly small changes in your data can have huge effects on coefficient estimates, thereby reducing their statistical reliability.
Inflated Models
Okay, so stochastic multicollinearity presents some hurdles if you’re wanting to make statistical inferences about your explanatory variables. Specifically, what it does is inflate the standard errors around your estimated coefficients which can result in a failure to reject the null hypothesis when a true effect is present (Type II error). Fortunately, statisticians have come to the rescue and have created some very useful tools to help diagnose multicollinearity.
One such tool is the variance inflation factor (VIF) which quantifies the severity of multicollinearity in a multiple regression model. Functionally, it measures the increase in the variance of an estimated coefficient when collinearity is present. So, for covariate j, the VIF is defined as follows:
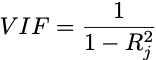
Here, the coefficient of determination is derived from the regression of covariate j against the remaining k — 1 variables.
The interpretation of the VIF is fairly straightforward, too. If the VIF is close to one this implies that covariate j is linearly independent of all other variables. Values greater than one are indicative of some degree of multicollinearity, whereas values between one and five are considered to exhibit mild to moderate multicollinearity. These variables may be left in the model, though some caution is required when interpreting their coefficients. I’ll get to this shortly. If the VIF is greater than five this suggests moderate to high multicollinearity, and you might want to consider leaving these variables out. If, however, the VIF > 10, you’d probably have a reasonable basis for dumping that variable.
A very nice property of the VIF is that its square root indexes the increase in the coefficient’s standard error. For example, if a variable has a VIF of 4, then its standard error will be 2 times larger than if it had zero correlation with all other predictors.
Okay, now the cautionary bit: if you do decide to retain variables that have a VIF > 1 then the magnitudes of the estimated coefficients no longer provide an entirely precise measure of impact. Recall that the regression coefficient for variable j reflects the expected change in the response, per unit increase in j alone, while holding all other variables constant. This interpretation breaks down if an association exists between explanatory variable j and several others because any change in j will not independently influence the response variable. The extent of this, of course, depends on how high the VIF is but it is certainly something to be aware of.
Design Issues
So far we have explored two rather problematic facets of multicollinearity:
1) Perfect multicollinearity: defines a deterministic relationship between covariates and produces a degenerate moments matrix, thereby making estimation via OLS impossible; and
2) Stochastic multicollinearity: covariates are approximately linearly dependent but the rank of the moments matrix is not affected. It does create some headaches in interpreting model coefficients and statistical inferences about them, particularly when the error term is small.
You’ll notice, though, that these issues only concern calculations about predictors — nothing has been said about the model itself. That’s because multicollinearity only affects the design matrix and not the overall fit of the model.
So…..problem, or not? Well, as I said at the beginning, it depends.
If all you’re interested in is how well your collection of explanatory variables predicts the response variable, then the model will still yield valid results, even if multicollinearity is present. However, if you want to make specific claims about individual predictors then multicollinearity is more of a problem; but if you’re aware of it you can take actions to mitigate its influence, and in a later post I’ll outline what those actions are.
In the meantime, I hope you found something useful in this post. If you have any questions, thoughts, or feedback, feel free to leave me a comment.
If you enjoyed this post and would like to stay up to date then please consider following me on Medium. This will ensure you don’t miss out on new content. You can also follow me on LinkedIn and Twitter if that’s more your thing 😉
Multicollinearity: Problem, or Not? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium
https://towardsdatascience.com/multicollinearity-problem-or-not-d4bd7a9cfb91?source=rss----7f60cf5620c9---4
via RiYo Analytics

No comments