https://ift.tt/HX7ehLq The history and potential use cases of quantum-derived technology Photo by Eilis Garvey on Unsplash Introducti...
The history and potential use cases of quantum-derived technology

Introduction
In the last few years, the miniaturization rate of general-purpose computer hardware has been limited due to exponential technical advances in component structure, efficiency, speed, and quality improvements. These changes were and are mainly encouraged by arising social necessities of communication, digital leisure, escape from real life and its problems, and work remotely due to a particular pandemic situation.
Hence, once a necessity has pushed science and technique to the edge, we start to encounter an insurmountable physical limit, the atom. Moreover, the inability to further reduce the size of classical processing devices has spread the belief that the trend supporting Moore’s law will flatten out in the following decades as engineer’s work will be much more complicated when building such tiny mechanisms. To properly understand what this means and why it’s going to happen, the smallest magnitude of a transistor, the most fundamental building block of classical computing, is about 2 nanometers. That means the tiniest virus found on earth is ten times bigger than the smallest transistor embedded in a CPU. Knowing that, it’s convenient to note that an atom’s diameter ranges between 0.1 and 0.5 nanometers, which is an insanely close distance we are approaching when producing high-end technology.

Size restrictions not only prevent CPUs from having more transistors and, thus, more computational power but also exclude them from being cheap or straightforward to build and repair due to their extraordinary complexity. Moreover, even if we could design a CPU that is a million times more powerful than today’s, it would be of little use if it required a million times more energy to run, introducing new issues to consider. So then, a solution proposed by many worldwide experts in computer science, physics, electronics, and mathematics is to build a so-called “quantum computer”. However, this idea of quantizing classical rules is not as contemporary as it seems. The first person to introduce it was Paul Benioff, a notorious American physicist widely considered the father of quantum computing. In his 1981 paper “The Computer as a Physical System”, he proposed the idea of a “quantum Turing machine” that would use the principles of quantum mechanics to perform computation. Though, it was not until 1995 that NIST researchers Christopher Monroe and David Wineland experimentally realized the first quantum logic gate, the controlled-NOT (C-NOT) gate, which led to the creation of the first working 2-qubit NMR (Nuclear magnetic resonance) quantum computer in 1998.
After spending more than two decades developing new approaches to the experimental realization of quantum logic gates and demonstrating their feasibility in the lab, scientific teams worldwide have successfully constructed quantum processors in various quantum platforms, ranging from trapped ions to superconducting circuits. In addition, its rapid growth has also made quantum computation a viable option for solving some of the most challenging problems humankind face. Nevertheless, the short time this field has existed has played to its disadvantage. Many hardware developers, researchers, and physicists who have dreamed of upgrading this world have faced a massive amount of hindrances and setbacks; the majority of them originated from the specific knowledge required to understand the working principles of a different way of handling physical elements to generate functional hardware applicable in industry. Therefore, the relationship between non-experts and quantum technology is likely to be one where the former group looks to the latter for potential solutions to problems, understanding that there may be a great deal of difficulty in implementing these ideas.
So, these fast progressions result in a prominent unawareness by the general public, sometimes overwhelmed by its contrast to the apparent simplicity of ancient technology from the 20th century or earlier. Besides the long-term adverse effects on certain groups of people who are currently being left behind when it comes to technological education, there are increasingly more issues related to its impact on the planet, the environment, and, therefore, all of us. Releasing products as advanced as the ones we have on the market, not only in electronics or computation but in all areas, implies the expenditure of a lot of resources and the production of waste, which can have severe consequences for our physical well-being. Since we won’t be able to completely solve this problem in a short period of time, we need to take advantage of today’s ideas, projects, innovations, and people’s will to achieve a sustainable way of existence.
Objective
This article aims to explain the fundamentals of quantum mechanics, quantum computation, and its blend with machine learning as simple as possible, providing an overall view of those research fields in order to resolve the question proposed in the title “Can Quantum Machine Learning help us solve climate change?”. By doing so, we can increase society’s knowledge and trust in these distant and disruptive tools, supposing an excellent opportunity to learn, contribute, and raise awareness about its possible use cases, mainly in the environmental care scope. Additionally, reducing the inextricable advanced concepts bounded to language and mathematics to something more familiar also provides a gateway to further studies and experimentation, essential for maintaining an intensive technological progression rate without causing a drawback to other aspects of society.
As possibilities are endless when dealing with such a necessary field to investigate as quantum mechanics, having a grasp of the basics forces us to adapt the mental framework with which we conceive of knowledge and gives us a deeper understanding of the universe we live in.
Basic concepts
History:
Before we jump right into the quantum computing concepts, we need to understand the physical principles that underlie and support its hardware. First, let’s discover the history of how it began to be studied. Early in the 20th century, physics consisted of three featured components, Newton mechanics, Maxwell electrodynamics, and Clausius-Boltzmann thermodynamics. Together, each of these branches of knowledge made up a complete explanation of known phenomena that was considered “classical physics” due to its deterministic nature. However, when it came to modeling the most fundamental aspects of the matter as the atomic spectrums, or situations near the speed of light, it incurred intense contradictions, which later led to Einstein’s Relativity Theory. Despite this, scientists kept searching for a unified physical theory that could consistently describe all natural phenomena through numerous experiments. Some of them inevitably brought us to the quantum mechanics we know today.
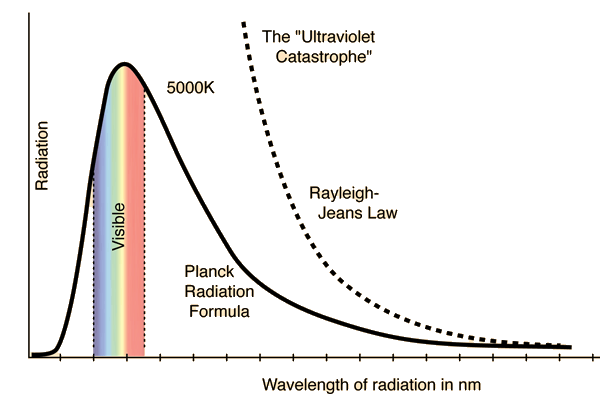
As an example, it is not superfluous to highlight transcendental problems like the Ultraviolet catastrophe, in which one was trying to find a law that would model the amount of radiation emitted by an ideal black body. This physical object absorbs all kinds of radiation in relation to its wavelength. As you can see on the above graph, the function represents the wavelength of the “light” emitted by an object corresponding to its temperature in kelvin degrees. For instance, if the object is not hot enough, it will irradiate infrared light, which humans can’t see without a proper detection device. Instead, objects with a temperature on the “Visible” stripe of the graph produce radiation we can perceive as light. For example, red-hot iron has a different color than a neutron star. When scientists tried to build this function with classical mechanics, two main approaches were proposed; the Rayleigh-Jeans law and Wien’s law, which failed to predict the correlation accurately. One of them tends to infinity when approaching low wavelength values, the other respectively when the wavelength approaches higher values.
As traditional physics solutions didn’t succeed, Max Planck decided to mathematically solve the problem by building a distribution that would accurately match most of the function values and then interpret its physical meaning. Planck, who is considered the father of quantum mechanics, reached the conclusion that energy is actually quantized, hence the name of the new branch of physics. In short, that means light (as well as energy) is cast and absorbed in tiny “packages” called quanta, not continuously as it was considered.
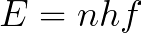
Finally, after quantum mechanics was born, nature started to be understood much better thanks to additional experiments like the photoelectric effect or the double-slit experience. Also, it encouraged theoretical development with works like Bohr’s postulates or DeBroglie’s hypothesis.
Fundamentals
If you want to know more about the origin of quantum mechanics, you can go to the resources section. But now, we will explore the theory behind the practical part of quantum computation.
A great deal of knowledge is based on the behavior of the electron, from velocity to spin. Modeling these parameters and knowing precisely its properties is crucial to operate at such close distances to the atom, where human perception and bias play a meaningful role in interpreting the sometimes odd results of the experiments and theoretical proofs. To introduce this “strange” working with which it’s known, let’s answer the question; What is an electron?. Since electrons are known, they have been defined as subatomic particles that make up an atom, together with protons or neutrons. The most exciting characteristic to know about them is their negative charge, which in contrast with the positive charge of protons, gives place to electrostatic interactions and subatomic forces like the electromagnetic, responsible for keeping electrons around the atom’s nucleus.
However, electrons become odd to study when we try to know their position, velocity, or angular momentum, also related to the popular spin or intrinsic angular momentum, which can be up or down in this case. So, if we ask ourselves about the electron’s location or velocity in space, we will have to deal with Heisenberg’s uncertainty principle, formalized as follows:
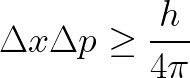
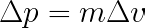
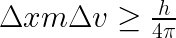
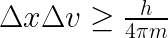
The above formulas relate Planck’s constant h with uncertainty quantities of position x and velocity v and tells us we can’t measure both variables simultaneously as they are conjugate (and connected by the Fourier Transform). But without entering so much detail about its proof, we can reduce and understand the concept by considering the following example: Imagine you have a moving object in space, and you take a very short exposition picture. In this case, you will know its position but not its velocity, as you aren’t able to determine where it’s going to move in the next step, so you have uncertainty on velocity. Instead, if you increase the exposition time of the camera, you will be able to know with certainty its speed, but this time position will be undetermined.
This phenomenon occurs with all possible conjugate variables we can extract from electrons, not only the ones mentioned before; position and momentum, energy and time, i.e., This idea of not being able to know simple parameters like position can seem counterintuitive, but we have to remember we are dealing with the most fundamental components of all matter. The macroscopic world is ruled by quantum laws too, but as Aristotle said;
A Whole is Greater Than the Sum of Its Parts
To conclude with the explanation of the basic mechanics, it’s essential to have the idea that matter does not always behave as particles but also as waves. DeBroglie introduced this hypothesis in 1924, and its core resides in the association of a specific wavelength to a particle depending on its momentum (velocity).
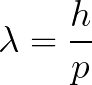
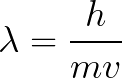
This hypothesis was made possible by experiments like the double-slit one, in which it was shown that measuring at quantum scales has profound effects. To know why it happens, we have to note that by nature, electrons are in a superposition state through which they can be simultaneously located in all positions belonging to a particular region of space. This superposition state is always conserved as long as we don’t measure it. If we try to observe its actual position, the state will collapse, and the electron will place itself in a point of space influenced by its wave function.
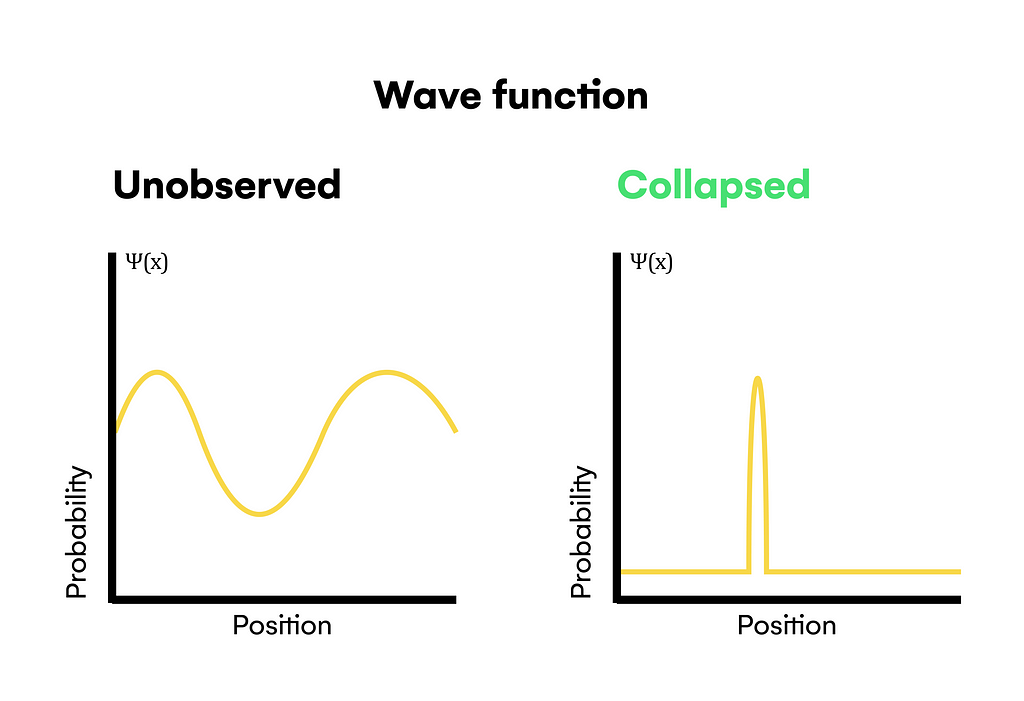
As you can see above, the wave function has a concrete shape that encapsulates the probability of finding the electron on a point in space (according to the Born rule), having a higher value when it’s more probable to find the electron and a lower value when the opposite occurs. Then, after measuring an exact position and breaking the superposition state, the wave function collapses into an alternative function with a peak at the point at which the electron was detected. This mathematical process has several physical interpretations like Copenhaguen Interpretation or Many-Worlds interpretation.
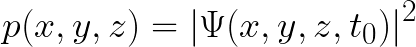
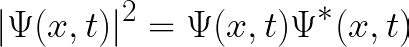
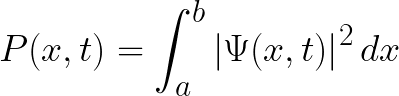
Knowing the position of an electron is necessary to understand its behavior in time. But before, we need to find its wave function Ψ(x, y, z, t), and the formal model responsible for making that possible is Schrodinger’s equation. Basically, it’s a linear differential equation used to get an appropriate wave function for a quantum system, which can be formed of individual subatomic particles or entire complex molecules. Each of these systems will have a different expression of Schrodinger’s equation and the cause of this variability is the Hamiltonian operator, the equation’s kernel:
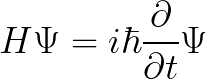
Hamiltonian is a physics operator which introduces the mechanical energy conservation principle to the equation, working similarly to classical physics.
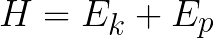
For example, if we have a Hydrogen atom as a quantum system and we want to know the movement of an electron inside it, the hamiltonian will be:
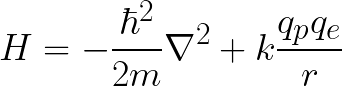
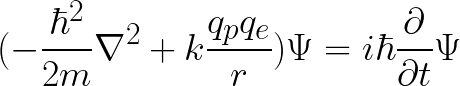
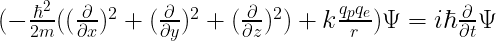
As this expression can become much more large and complex depending on the quantum system, there are several ways to come up with a suitable solution for the wave function; please visit the following resource to learn in detail how physicists solve it:
Classical Computation
We have seen that classical computing is approaching the atomic limit with several consequences, for example, the quantum tunneling effect. To comprehend its implications, let’s first define what a computer is in its simplest form.
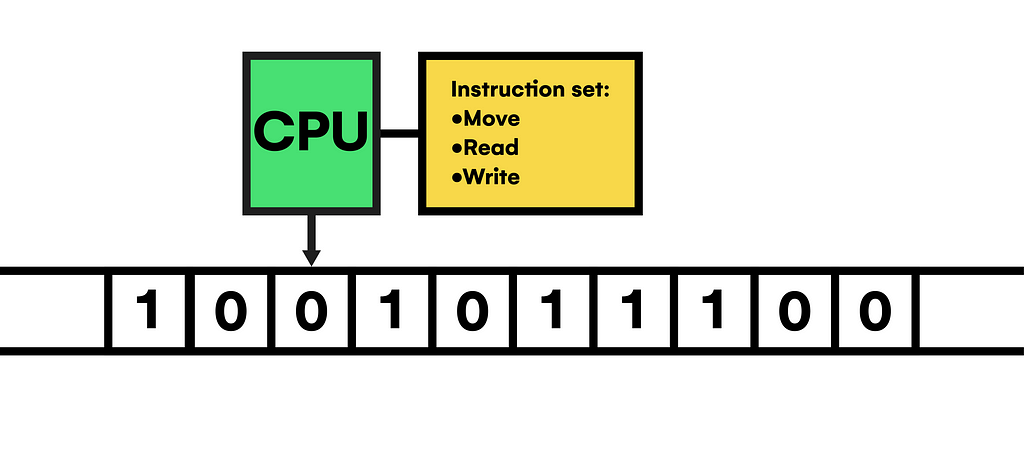
Also known as universal Turing machines, computers consist of a list of cells containing a discrete value represented formally as 0 or 1, called the main memory. Outside this storage, a header can slice through memory, reading and modifying the cell’s values directed by a set of instructions (program) encoded in a binary representation and stored in memory.
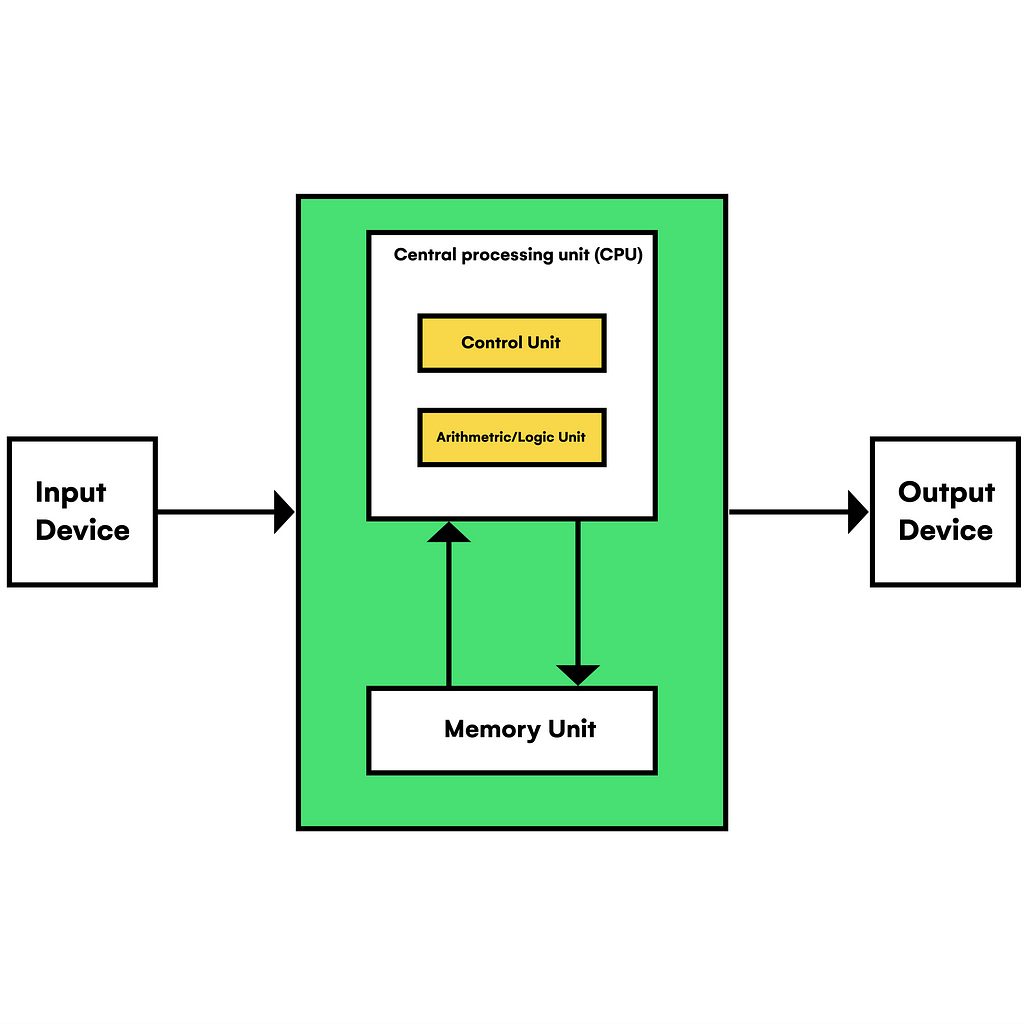
But practically, the formal representation of a computer is brought to reality by the Von Neumann architecture. Indeed, the list of cells is formed by the RAM and SSD/HDD disk drive. The header is a processing unit CPU (sometimes in combination with a GPU for parallelizable processes) made up of bistable and combinational circuits able to perform straightforward operations like summing, comparing quantities, counting, or registering. At the same time, as you can see in the documentation, these circuits contain logic gates, the building blocks of boolean algebra. Although, if we look closer to the atomic scale, we will see combinations of transistors representing the working of logic gates.
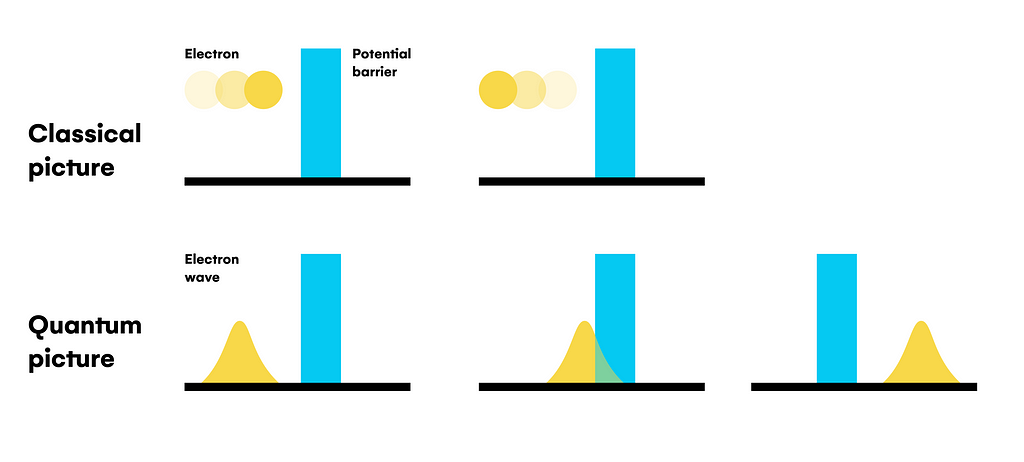
As transistors act as barriers allowing or preventing the flow of current (electrons), sometimes the particle-wave duality of the electron’s behavior causes current leaks in a process denoted as quantum tunneling, where the superposition state of the electron allows it to be in both sides of the barrier “simultaneously” despite of having a lower probability value on one side than the other, as you can see above. This effect implies execution issues and data corruption, which are mostly resolved with error correction algorithms, highlighting the Hamming code in computer science as the starting point of these algorithms.
Quantum Computation
The need for powerful error correction algorithms in quantum computing is significantly greater than in the rest of computer science systems due to the extreme conditions its hardware must keep.
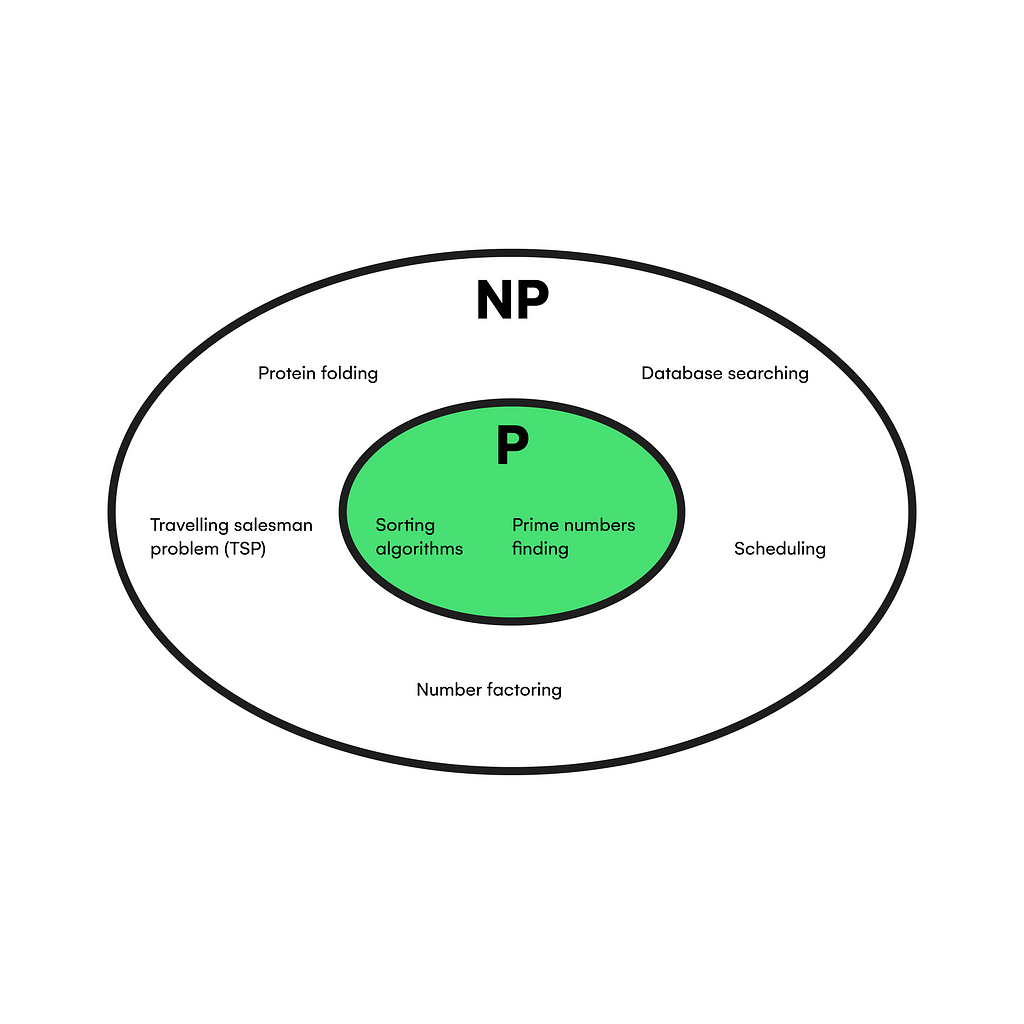
The main contrast between these types of computations resides in the nature of each memory cell containing discrete information. Although quantum computers use the same binary representation of data, they predominantly utilize superposition and entanglement quantum phenomena to expand the information processing capacitance crucial to approach NP complex problems much more efficiently than classical computers.
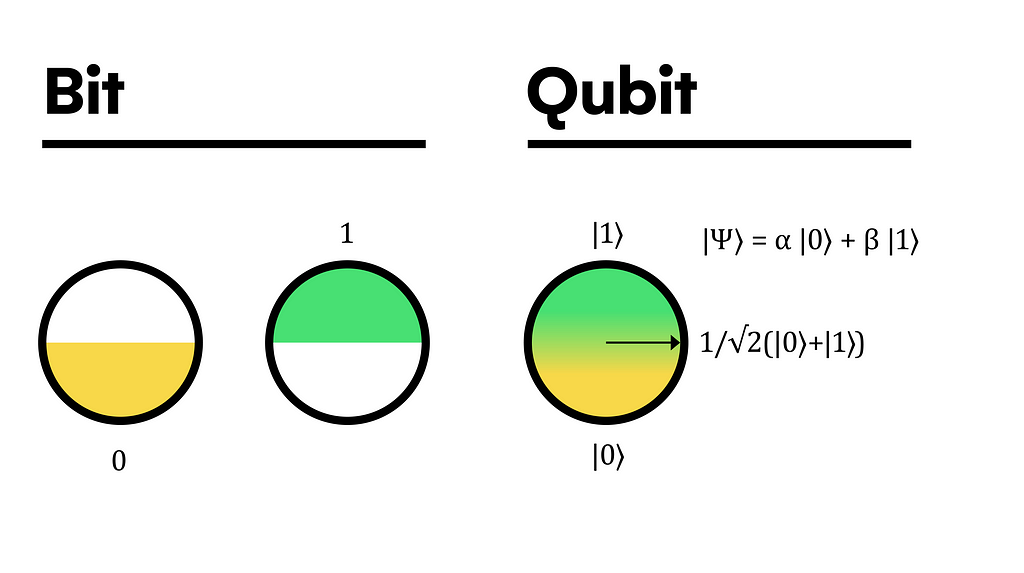
Briefly, while a classical bit (cell of memory) can be in one of the two basic states, a quantum bit (Qubit) has a third state labeled superposition in which it can take any linear combination of the basic states, having an uncertain value until measurement (break superposition of state) and fulfilling quantum mechanics rules.
Formally, the qubit’s states are depicted with Dirac’s notation. Thereby, the state of a qubit |Ψ⟩ is constituted by a combination of two complex coefficients, α and β, multiplied by the basic states|0⟩ and|1⟩, respectively. Thus, if we plot this information on a sphere known as Bloch’s sphere, we can have a better idea of what a qubit actually is.
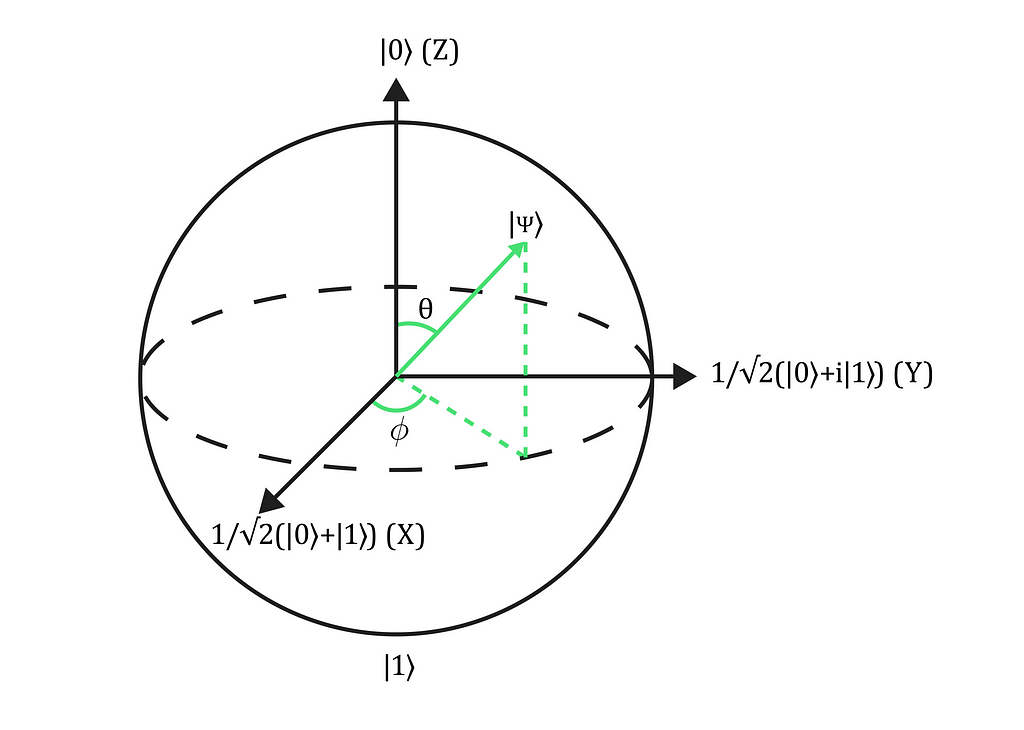
As you can infer, the closer the qubit is to |0⟩, the greater the corresponding coefficient is, and the same for |1⟩. Hence, we can observe that these numbers contain the probability of getting a specific basic state when breaking the superposition.
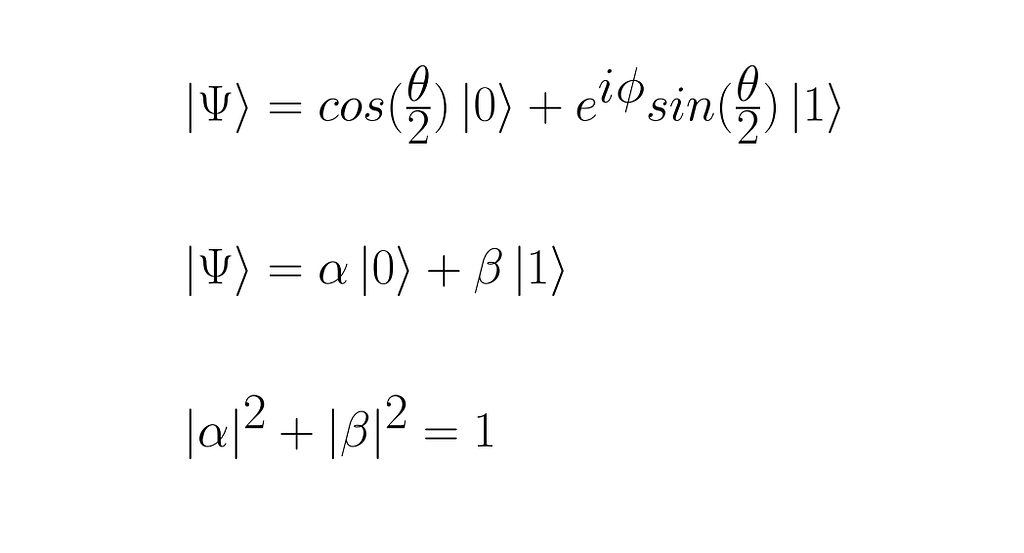
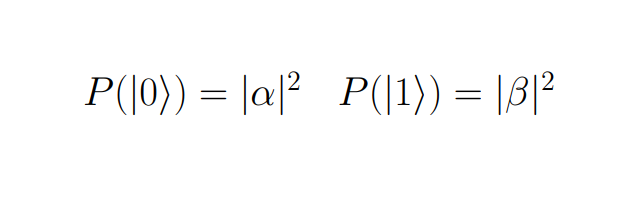
So far, this way of storing data may seem overcomplicated. Still, the key that makes quantum computers so fast in solving NP-Hard problems like factoring a large number is having multiple qubits in a quantum system. Despite the increase in hardware issues and the need for more robust error correction algorithms, multiple qubit systems take advantage of their superposition by linearly combining all possible basic state values of all system qubits simultaneously. So with n qubits, you will have 2 to the n coefficients (equivalent classical bits), all of them necessary to determine the superposition state of the quantum system.
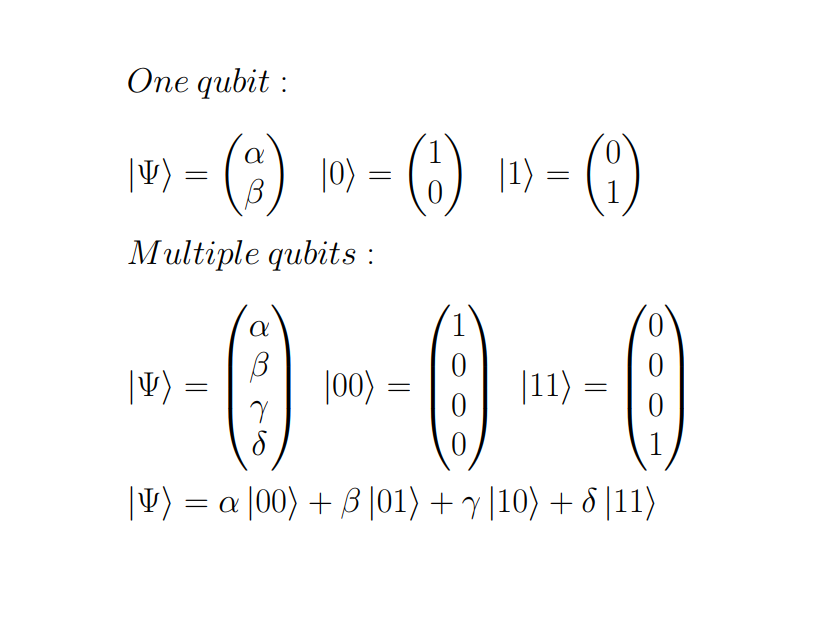
In the next section, quantum algorithms will help you understand the superposition utility at its best.
Quantum Algorithms
It has been known for several years that quantum computers would be able to break the RSA encryption protocol with Shor’s algorithm and powerful enough computers. But, why is superposition key when solving such tasks?. The answer is simple; a quantum computer can generate all possible answers to a problem by superposing multiple qubits and discard “wrong” solutions by destructively interfering with superpositions as if they were “waves”.
To build quantum algorithms, similarly to classical computing, we need to transform initial state qubits to a final state by sequentially disposing of logic gates in a circuit.
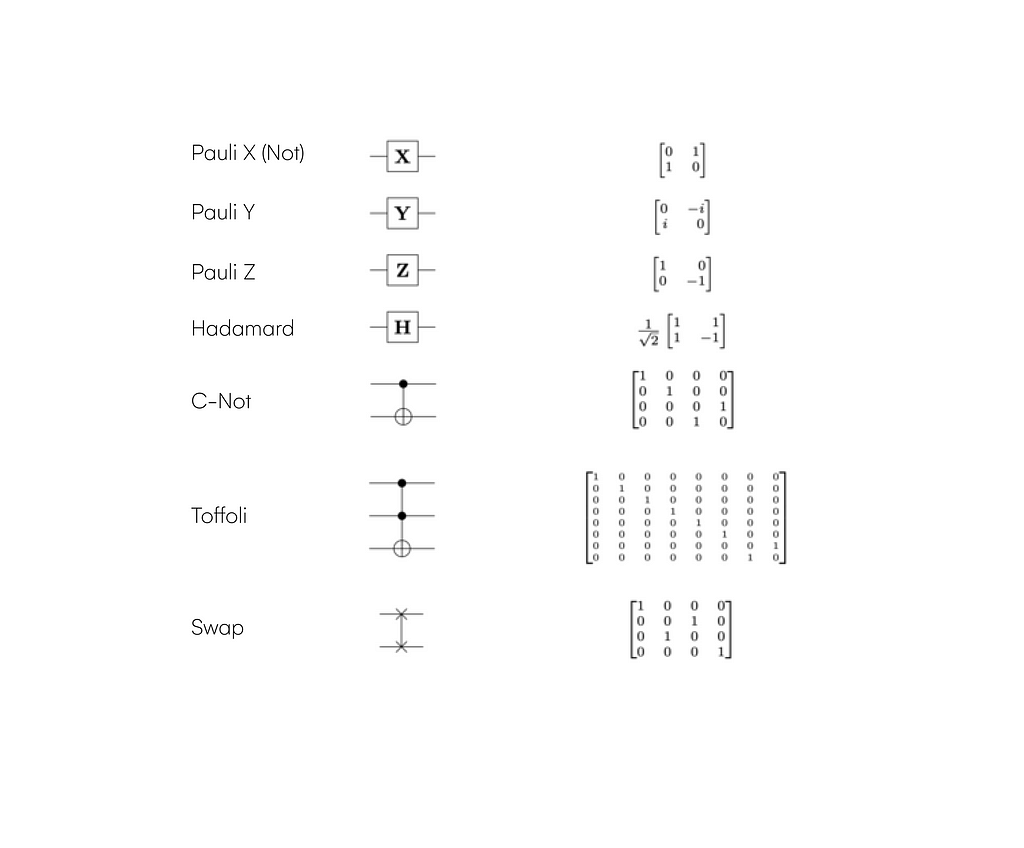
Above, you can see the leading gates present in most algorithms. For example, X-Gate is an equivalent of logical negation; meanwhile, Hadamard/ C-Not gates introduce superposition and entanglement, respectively. You can learn more at Qiskit’s official guide to have a complete explanation of its working and relation with classical gates. Nevertheless, it’s necessary to stand out that all quantum gates are reversible unitary matrices, making quantum computation processes reversible. Also, quantum computers are the only devices that can generate a truly random number with a circuit as simple as this:
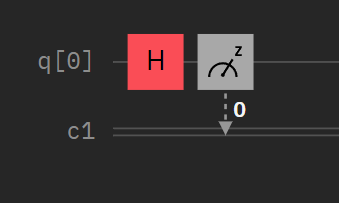
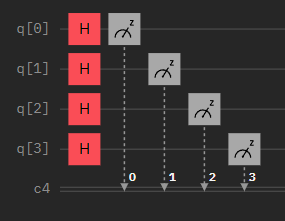
As an example of efficiency improvement over classical computing, imagine that you have a boolean function f(x) {0, 1}→{0, 1} and you want to know if it’s constant or balanced. With a classical computer, you would evaluate the function in 0 and 1 and compare the results if the function is not computationally expensive. If it is, you may need to use Deutsch’s algorithm to exponentially increase your program’s time performance by avoiding the second evaluation of the function.
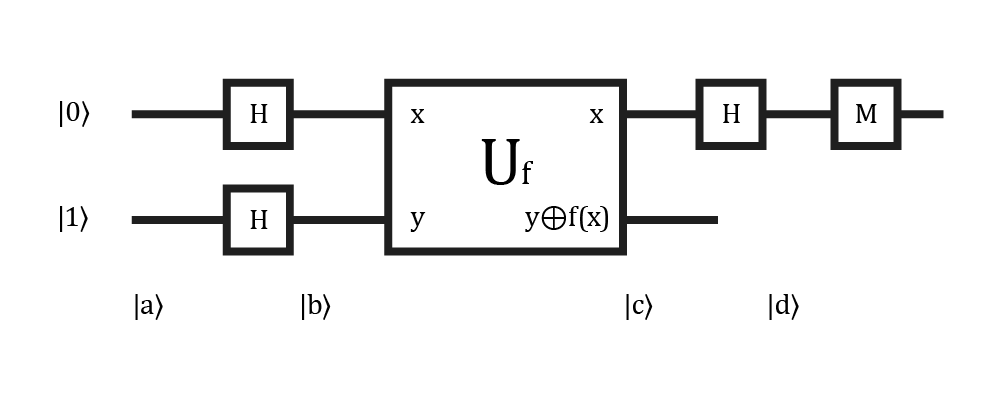
Formally, it’s proven that the upper qubit’s state at the end of the process will be |0⟩ if f(x) is constant and |1⟩ if not. But, to clearly understand what the algorithm is doing, we can split the process into four pieces. First, all qubits are initialized |a⟩ and set into a superposition state with Hadamard gates |b⟩. Then, U acts as a C-Not gate to traverse all possible combinations of the input values, adding the function as the main component to the superposition processing |c⟩. Lastly |d⟩, another Hadamard breaks the superposition of the first qubit, and it’s measured to complete the task.
Quantum Machine Learning
This section deserves special attention because it is still under development and has diverse approaches depending on the problem type. Therefore, here we will only focus on the basics of neural networks, the most prominent technique for the near future.
First, we need to know that the intersection between machine learning and quantum computation fields generates four working methods depending on the data and algorithm’s type.
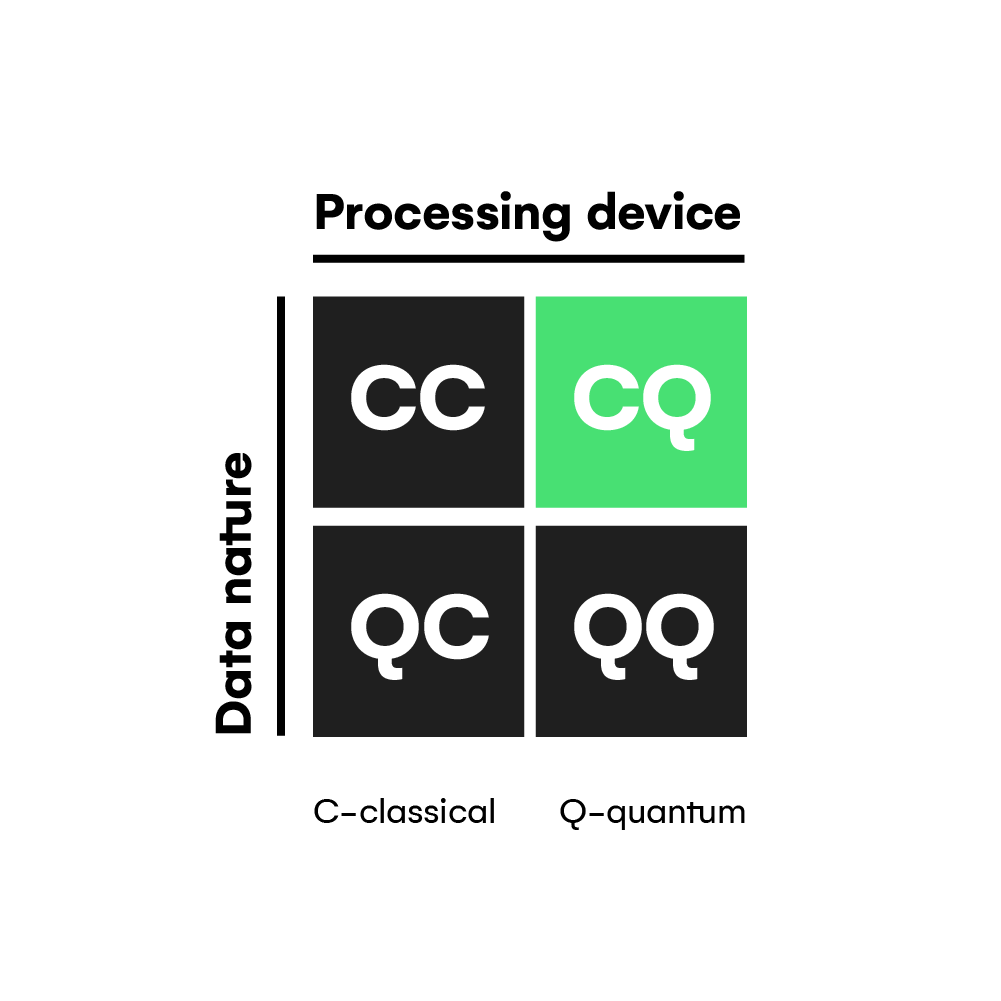
According to the diagram, we can have hybrid systems where classical and quantum computers work together to encode data and optimize machine learning models. Of course, quantizing one or both processes has its own advantages. For instance, if your classical model is too deep and costly to traverse when training, you may want to use a quantum model’s superposition to improve execution times, leaving other tasks such as parameter tuning to a classical device.
As data is crucial to sustain this workflow, a wide range of statistical processes aim to extract patterns from data. But neural networks deserve to be highlighted due to their excellent generalization capability proven in theorems like the Universal approximation theorem. Succinctly, they are differentiable mathematical models in which a training process is used to modify their parameters so that the model fits the patterns of an input data set.
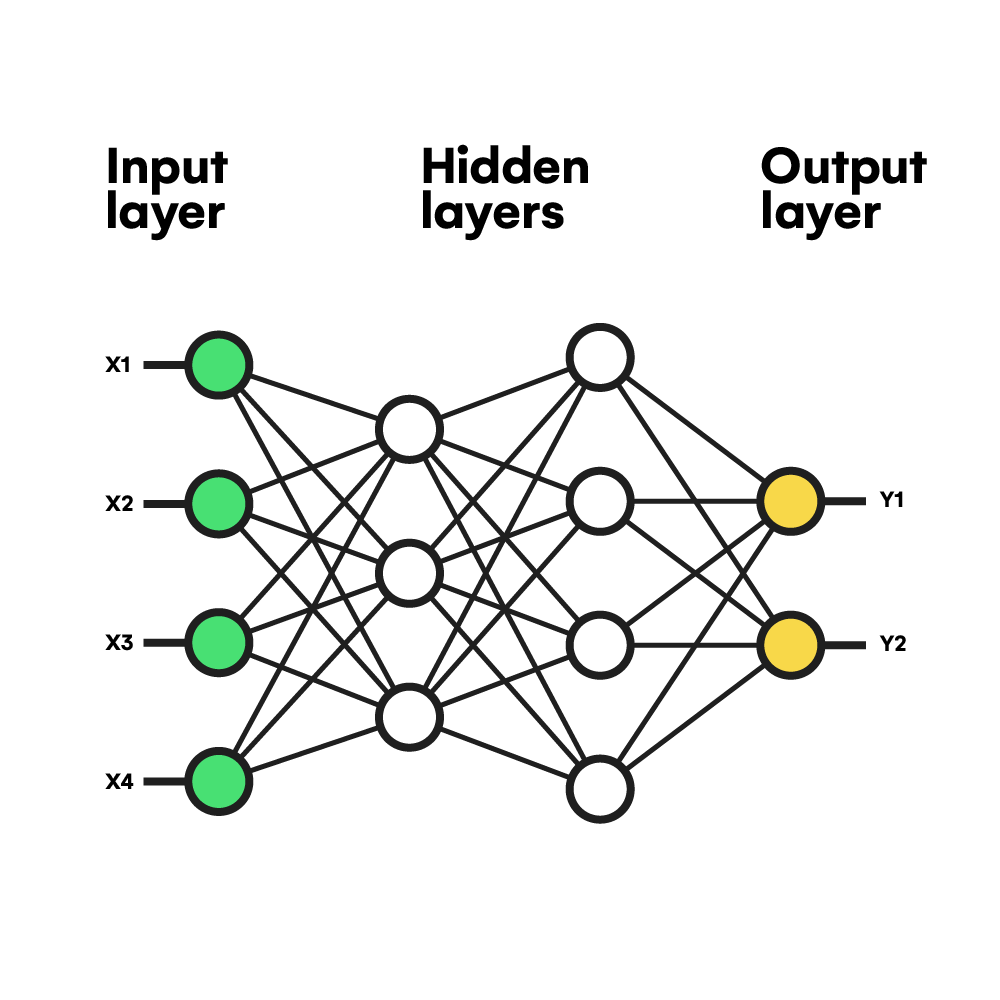
As you can see in the above representation from this article, neural networks try to mimic the brain’s functioning by concatenating layers of perceptrons (neurons), which are functions containing variable parameters. Then, to test the model’s effectiveness in fitting a particular input dataset, a cost function is calculated and minimized in every training iteration to achieve an “intelligent” model that later performs inference outside the training data.
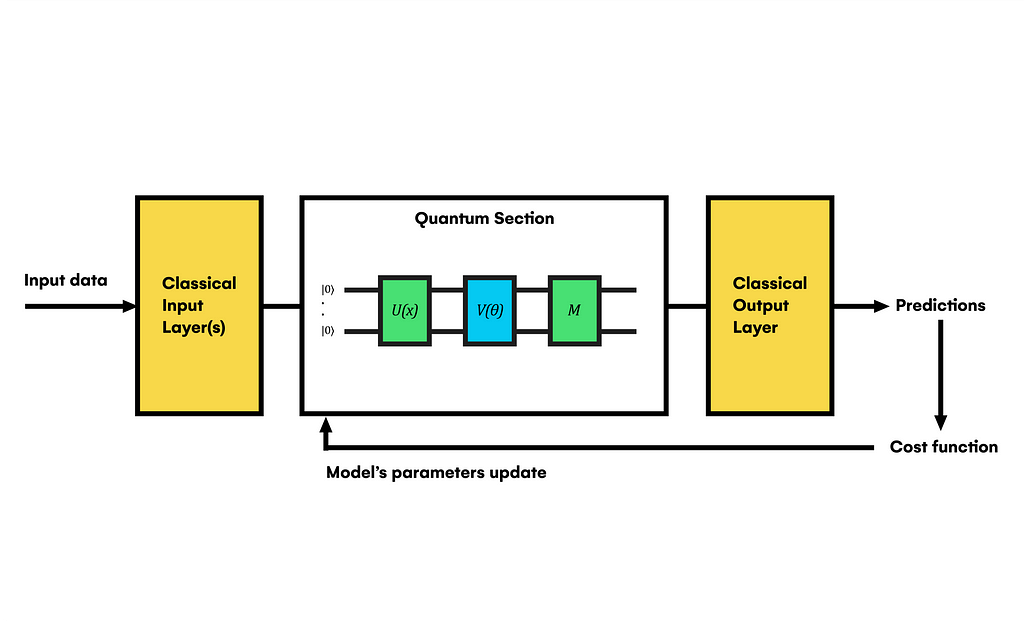
In the case of quantum neural networks, the main difference is the computation of the model for each training iteration, accelerating the process and its generalization capability by relying on quantum superposition and entanglement. Here, you must input classical data into a quantum circuit, encoding that data with U(x) gates block from |0⟩ initialized qubits. Next, correctly formatted data is fed to the differentiable model V(θ) in a superposition state and classically measured to get an output used to minimize the cost function and tune the model’s parameters (θ).
This was a simplified example of the essence of quantum machine learning. But since it is such a broad field, you can continue to learn more about it here.
Applications
Fundamentally, humans have been trying to simulate physical elements like atoms on classical computers almost since their creation. However, this task becomes exponentially costly from a computational standpoint when dealing with systems with many molecules. For this reason, quantum computers have begun to be used in various research projects aimed at faithfully modeling interactions between matter to gain new knowledge and develop products with superior performance in the marketplace and new ways of communication which will have a notorious impact on our lives.
Concerning climate change and environmental care, simulating a physical system by successfully including the laws of quantum physics implies the creation of new materials such as graphene or any other whose properties allow it to be fully recycled. For example, plastic, the planet’s primary residue-generating material, could be replaced by another whose properties contribute to its proper reuse/decomposition or modified to make it more sustainable. Moreover, since the planet is already polluted to some extent, recycling plants that rely on classical machine learning models to sort waste will benefit from using quantum models. They will improve their efficiency, work rate, and accuracy, avoiding waste accumulation issues.
Materials may have an impact on nature, but CO2 emissions are certainly one of the main accelerator components of the greenhouse effect and climate change. In this respect, it’s proven that quantum computers are extremely suitable when performing route optimization by solving problems like TSP, which would reduce vehicle emissions. However, the automation advantages they offer and the possible development of highly durable batteries are the most interesting applications for almost all industries, as they would put an end to global harmful emissions. All of this assuming that the minority of industries harmed by those improvements (oil companies, among many others) don’t forcibly prevent the proper development of the technology for purely economic purposes.
In conjunction with other applications such as the launch of new drugs, the improvement of healthcare techniques, the cure for cancer, and a better understanding of the human brain and DNA, initiatives such as JoinUs4ThePlanet are willing to use disruptive technologies to raise awareness about sustainable consumption and contribute to technological development aimed at preserving our environment.
Conclusion
Back to the title’s question, we can state that quantum computation can contribute to almost any area of our lives, including climate change fighting. Also, we must note that it’s a paradigm that needs the classical framework to achieve a beneficial result when solving a complex task. Thus, considering it as a complement to classical computing suitable only for heavy processes, we can conclude that there is still a lot of work to be done, which we will have to do together so that quantum computing becomes a comprehensive but safe, understandable and game-changing tool.
Can Quantum Machine Learning Help Us Solve Climate Change? was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/Mu5P3qF
via RiYo Analytics

No comments