https://ift.tt/SvPqcFx Considering the “Invisible Gap” between Measurements and their Meaning In an era of empiricism, where insights that...
Considering the “Invisible Gap” between Measurements and their Meaning
In an era of empiricism, where insights that are “data-driven” are automatically deemed superior, quantification is vital. Indeed, the measurement of constructs and phenomena is at the core of empirical science, research, and reasoning. However, this quantification is often challenging, and is interrogated accordingly during the research process. Nevertheless, the criteria for “good” quantification are arguably agreed upon; These goals are the minimization of bias and variance.
During a visit to HEC Paris, Nobel laureate Daniel Kahneman spoke of the consequences of both both bias, evoked heavily in Thinking, Fast and Slow, as well as noise, which has been the subject of his more recent writing. During his talk, I raised questions on whether the focus on the aforementioned dichotomy may cause us to overlook certain flaws in empirical models. With the luxury of further reflection and more space to articulate these thoughts, I would like to elaborate on my concerns in this article.
Bias and variance: A short but necessary overview
To model a phenomenon, empirical research frameworks rely on various approaches to measuring a construct within the population. As an example, one may want to measure the danger to health posed by coronavirus. To achieve this, one might obtain death rates (i.e., samples) from various hospitals , and average them to achieve our true goal of estimating the death rate in the overall population. One would then hope that this approach to estimating the overall death rate has low bias, and low variance, and that bias and variance decrease as the number of observations increases. However, the figure below illustrates the key issues that could arise during this estimation process.
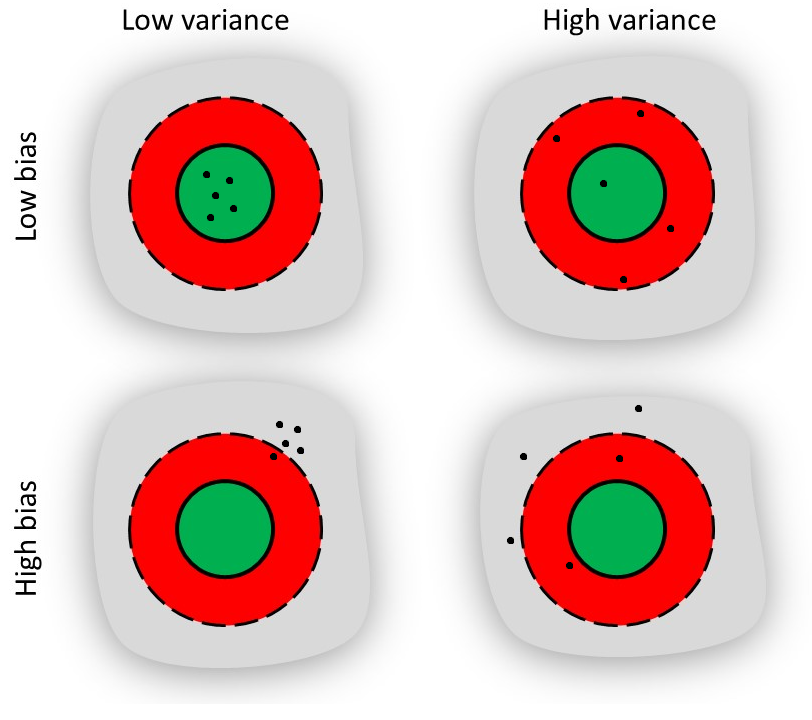
One issue may be that the estimator has high variance (top-right), meaning that sample hospitals vary significantly in the death rates they report, despite being dispersed around the “true” population death rate. Such a result would indicate that the estimation of the true death rate are scattered, loosely-speaking. Another issue would be if the estimation process is biased (bottom-left), meaning that it consistently skews estimations in a certain direction. Perhaps, for example, our approach involved sampling hospitals in poor areas, which might exhibit higher death rates due to inferior medical resources. Combining these two issues, an estimator may be both biased and exhibit high variance (bottom-right).
Motivated by our tacit imperative to minimize both bias and variance, perhaps the most commonly used model in empirical research is ordinary least squares regression (a.k.a. OLS). Depicted below, this approach essentially takes in data, and finds a trend line that minimizes the total error between the line and data points it represents (i.e., the “sum of squared errors”). According to the Gauss-Markov Theorem, the OLS approach is BLUE — i.e., the best linear unbiased approach to modeling such phenomena, meaning that it is the approach that yields minimal bias and variance. Building more sophisticated and non-linear models, empirical researchers consider the bias-variance tradeoff, again with the goal of minimizing these values. Hence, the selection of an empirical modelling approach is guided heavily by the minimization of bias and variance.
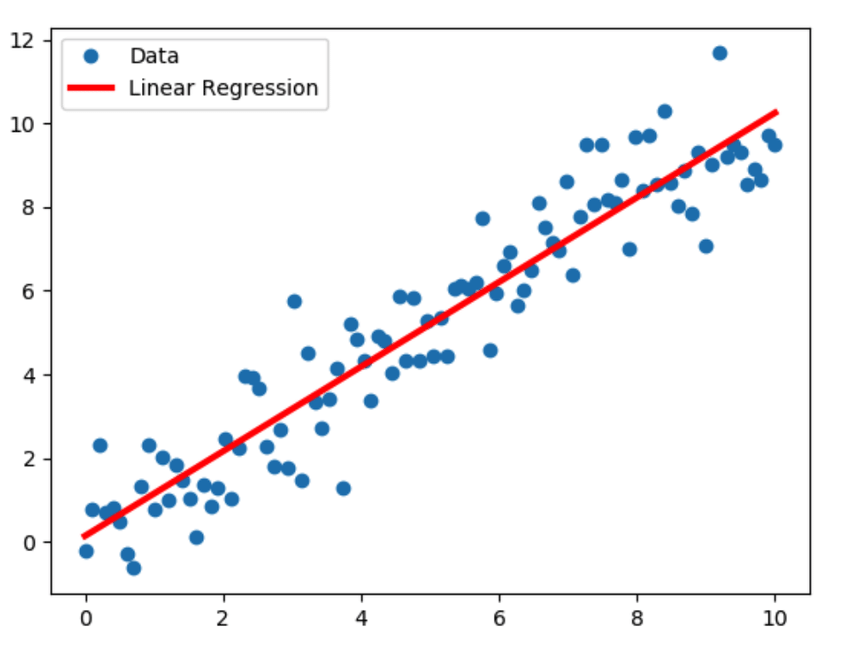
My argument would be that, being blinded by the minimization of bias and variance, we often miss a more fundamental question: what is the underlying target? What are those points on the regression chart above? After all, discussions of either of these factors are less relevant if the target is poorly defined. Often, we do not dig deep enough into this target, but rather accept the metric that most easily affords quantification.
Is there ever a “true” target?
In the example of coronavirus death rates, let us consider the context in which we might be interested in such a metric. In this particular case, it is likely that the science behind this estimation would be intended to inform decisions or policies. For example, a death rate may influence individual decisions on vaccination, or policies on lockdowns. A model that focuses on death rate as an outcome would hence offer prescriptions to optimize (in this case, minimize) this pre-determined metric.
Even with an accurate (i.e., low bias, low variance) estimate of death rate, this metric is only one of numerous factors one could have considered in the broader context of minimizing harm or maximizing general health. Thus, death rate is a proxy for an underlying construct of interest, such as general welfare. Even with the gap between “true” death rate and measured death rate being minimal, there can remain an invisible gap between our chosen metric and the true target for which this metric is a proxy.

By failing to consider the distance between a metric used and the true construct of interest, we run the risk of being seduced by the simplicity of quantification. For instance, one may seem rigorous by citing a low death rate as an outcome of interest and proposing policies accordingly (e.g., eliminate lockdowns). Indeed, this was an argument used by libertarian voices, who often seem to brand themselves as the “reasonable” and “objective” ones, as compared with others such as liberals. However, to counter such an argument, one need not rely on questioning the accuracy of the measurement; Rather, a better strategy might be to question the choice of metric itself.
Given the potential loss of information resulting from one’s choice of metric, one might ask: can a quantifiable measurement be the “true” target? This question is analogous to the popular question: “Is everything quantifiable?”. Indeed, on the one hand, one can construct a metric to associate with anything; However, in doing so, one inevitably loses nuance in representing the more abstract construct that they truly wish to represent. Even in cases where an idea is cleanly measurable (e.g., weight, population), very rarely are we actually interested in such a simplistic construct as such. Rather, it is more likely we use a measure like weight as a representation for a more abstract and multi-dimensional concept like “health”.
Moving beyond bias and variance
While the focus of empirical science has been in establishing accurate measurement scales, research can also benefit from reflecting upon the underlying construct of choice, as well as the choice of metric as a proxy. Ignoring such questions would give the illusion that the scientific process is grounded in objective measurements. However, the choice of measures as a proxy for the true underlying construct is very often subjective, and can be manipulated to serve a specific agenda (e.g., elimination of lockdowns based on low death rates).
In spite of these issues, there may be occasions in which the loss of nuance associated with quantification is acceptable. For instance, when I publish a paper where the phenomenon of interest is the consumption of online videos, one might ask questions such as: Did they view the entire video? How much attention were they paying to this video? One can make similar analogies in practice, for instance if a firm is monitoring “visits” to its website. While quantifying such constructs using a simple tally may lose nuance, some information loss is necessary to construct empirical models, which are abstractions that can guide our actions and decisions.
Beyond the world of science, we can improve the way we frame our models in common parlance. Even casual statements we hear in daily life such as “I am biased” should be examined — what exactly are you biased towards or against? What is the true construct you are trying to evaluate, and why do you assume that the process through which you arrived at your preference is distorted? If the issue itself is inherently subjective (e.g., I am biased because I am a fan of the Paris Saint-Germain football club), then the word “biased” is misused because there is no “true” target being estimated, irrespective of measurement challenges. Alternatively, if the bias is towards a preference that one arrives at systematically (e.g., As a supporter of Emmanuel Macron, I am biased), then one should ask what is preventing this person from conducting their analysis differently.
With the rise of quantification and favoritism towards “objective” analyses, we run the risk of ignoring philosophical issues such as the gap between measures and their theoretical targets. While even discussing this gap requires us to enter a messier realm of nuanced subjectivity, it is better to do this explicitly than sweep the mess under the rug implicitly. It would be useful for scientists to consider developing guidelines around this practice to ultimately make their empirical analyses more convincing.
Beyond Bias & Variance was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/I6TLiFJ
via RiYo Analytics

ليست هناك تعليقات