https://ift.tt/4lsN2mR The fastest and most intuitive unsupervised clustering algorithm. Clusters Image — By Author In this article, we...
The fastest and most intuitive unsupervised clustering algorithm.

In this article, we will go through the k-means clustering algorithm. We will first start looking at how the algorithm works, then we will implement it using NumPy, and finally, we will look at implementing it using Scikit-learn.
Introduction
K-means clustering is an unsupervised algorithm that groups unlabelled data into different clusters. The K in its title represents the number of clusters that will be created. This is something that should be known prior to the model training. For example, if K=4 then 4 clusters would be created, and if K=7 then 7 clusters would be created. The k-means algorithm is used in fraud detection, error detection, and confirming existing clusters in the real world.
The algorithm is centroid-based, meaning that each data point is assigned to the cluster with the closest centroid. This algorithm can be used for any number of dimensions as we calculate the distance to centroids using the euclidian distance. More on this in the next section.
The benefits of the k-means algorithm are that it is easy to implement, it scales to large datasets, it will always converge, and it fits clusters with varying shapes and sizes. Some disadvantages of the model are that the number of clusters is chosen manually, the clusters are dependent on initial values, and that it is sensitive to outliers.
K-means Steps
The steps of training a K-means model can be broken down into 6 steps.
Step 1: Determine the number of clusters (K=?)
It is best if K is known before model training, but if not, there are strategies to find K. The most common is the elbow method, which plots the sum of the squared distances as K increases. By looking at the plot, there should be a point where increasing the size of the cluster provides minimal gain to the error function. This is known as the elbow and should be chosen as the value for K. This is shown in the following graphic.
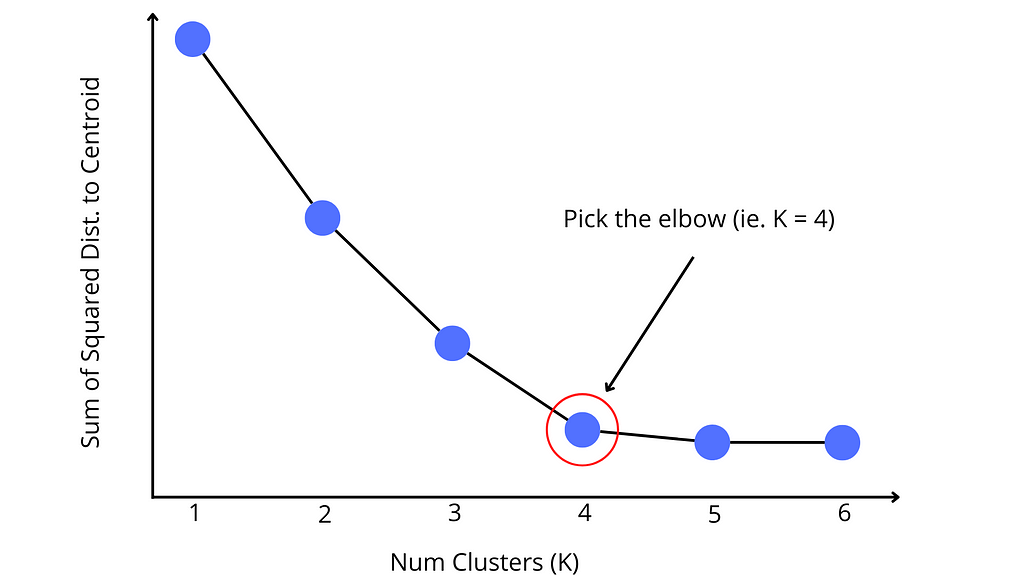
Step 2: Initialize cluster centroids
The next step is to initiate K centroids as the centers of each cluster. The most common initialization strategy is called Forgy Initialization. This is when the centroids for each cluster are initiated as random data points from the dataset. This converges quicker than random initialization as clusters are more likely to be present near data points.
More complex strategies like k-means++ initialization aim to choose initial points that are as far from each other as possible. This strategy has proven to be the best initialization method for the k-means algorithm. You can see the mathematics behind k-means++ here.
Step 3: Assign data points to clusters
After initializing K clusters, each data point is assigned to a cluster. This is done by iterating over all the points in the data and calculating the euclidian distance to each centroid. The formula for euclidian distance works with any two points in n-dimensional euclidian space. This means that a data point with any number of dimensions is assigned to the closest cluster.
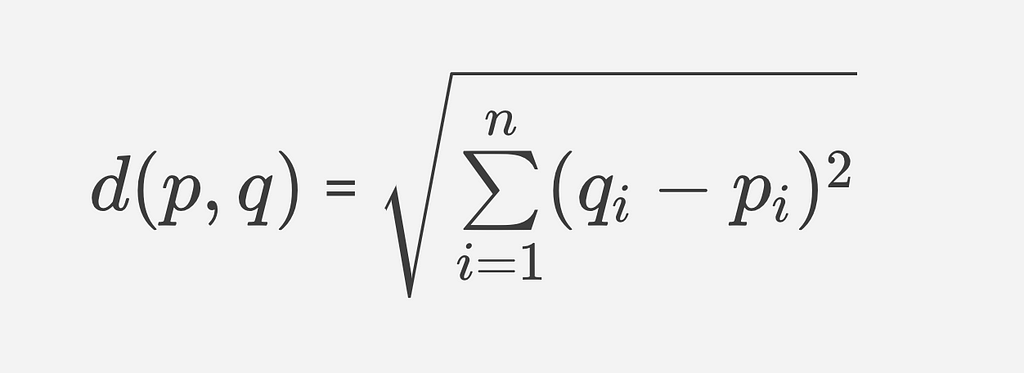
Step 4: Update cluster centroids
Once each data point is assigned to a cluster we can update the centroids of each cluster. This is done by taking the mean value of each data point in the cluster and assigning the result as the new center of the cluster.
Step 5: Iteratively Update
Then, using the newly calculated centroids we go through all the data points and re-assign them to clusters and re-calculate the centroids. This is done repeatedly until the centroid values do not change.
The beauty of the k-means algorithm is that it is guaranteed to converge. This is a blessing and a curse as the model may converge to a local minimum rather than a global minimum. This idea will be illustrated in the following section where we implement the algorithm using Numpy, followed by the implementation in Scikit-learn.
K-Means: Numpy
First, we will import the necessary python packages and create a 2-dimensional data set using Scikit-learn’s make_blob function. For this article, we will be generating 300 data points that are distributed amongst 4 clusters. The generated data is shown below.
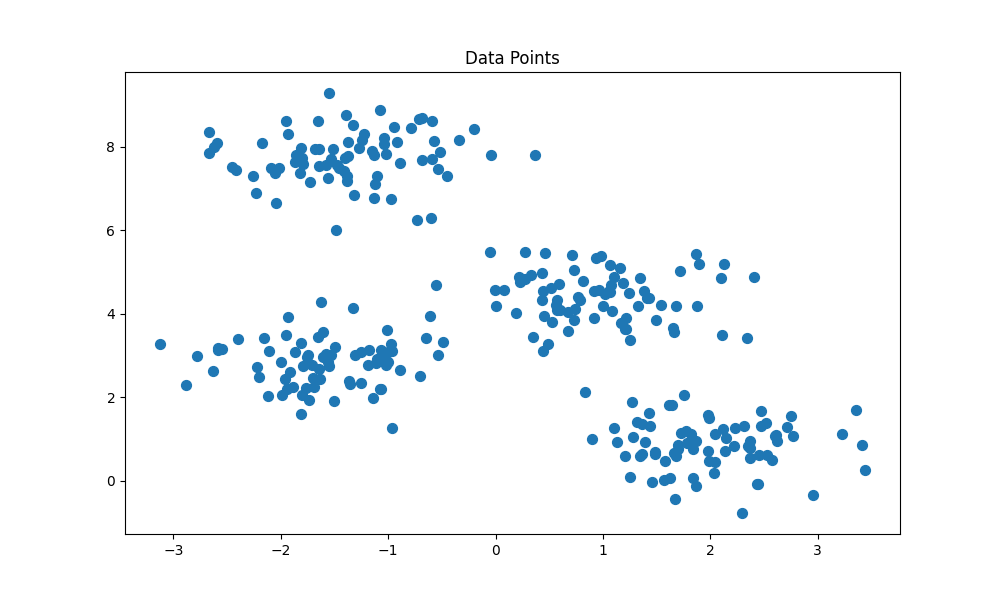
We can see that there are 4 distinct clusters in the sample, with a slight overlap between outlying data points in each cluster. Next, we will initiate two hash maps. One will keep track of the cluster centroids, and the other will keep track of the data points in each cluster.
Now that the centroids are initialized, we will define three more functions. The first takes in two data points and calculates the euclidian distance. The second function updates the centroids of each cluster, and the final function assigns data points to each cluster.
The final three functions put it all together by providing a means to check if the model has converged, to have a master training function, and to visualize the model results.
So putting together all the functions above, we can train the model and visualize our results in two lines of code. By implementing the algorithm using functional programming, we are able to make the code readable, limit repetition, and facilitate improvements to the code.
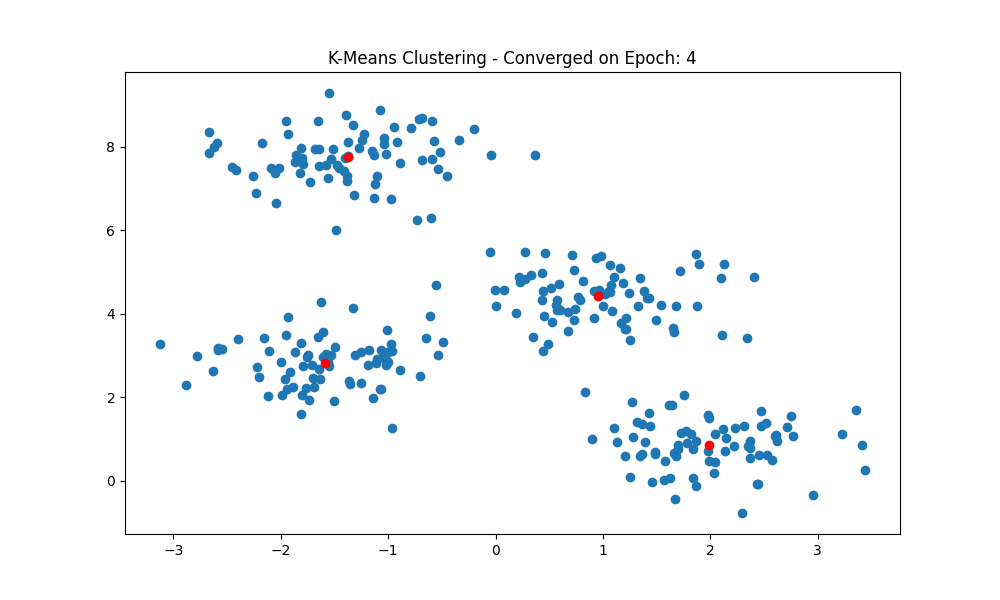
In the model training above, we saw that the model was able to converge after 4 epochs and correctly identified the clusters we generated. That’s pretty good, but the result of the generated clusters is highly dependent on the initial centroids. If we train the model multiple times with different initial centroids, we can see how the model converges to a different minimum on the different training cycles. This is where K-means++ initialization can be useful as it increases the likelihood of converging to the global minimum.
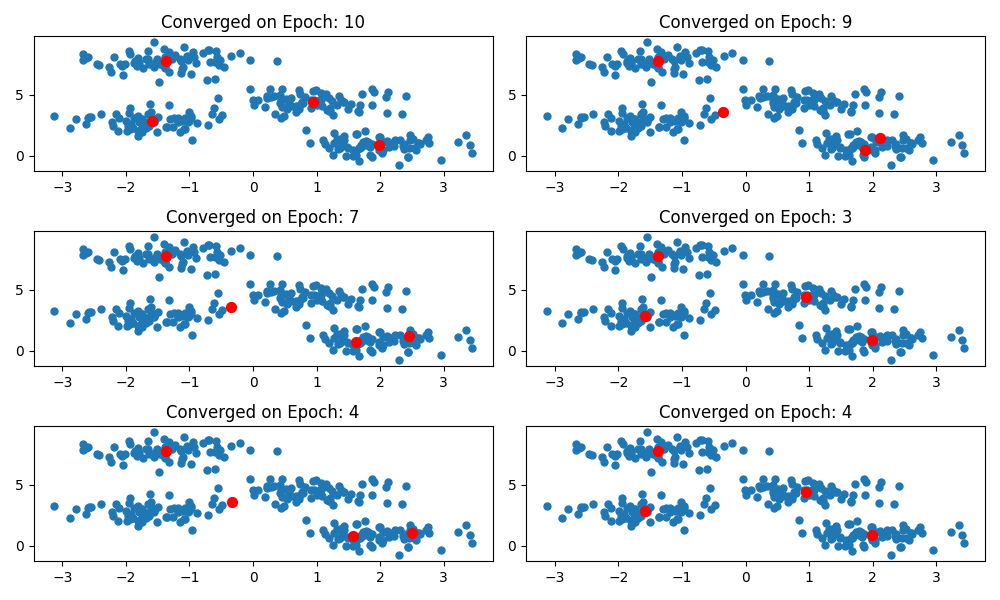
Great! Now we were able to implement the k-means algorithm from scratch, but is this feasible in the real world? Not really. In the real world, you are more likely to use existing model libraries like Scikit-learn to train, test, and deploy models.
K-Means: Scikit-Learn
The benefits of using existing libraries are that they are optimized to reduce training time, they often come with many parameters, and they require much less code to implement. Scikit-learn also contains many other machine learning models, and accessing different models is done using a consistent syntax.
In the following cell, we implement the same k-means clustering algorithm as above, except that by default we are initializing the centroids using k-means++. All this is done in under 20 lines of code!
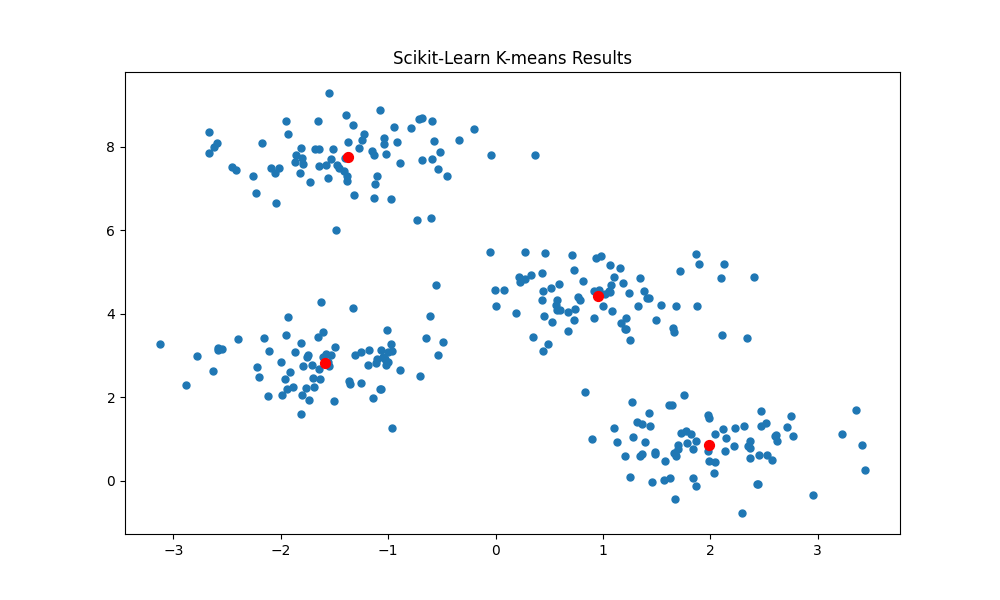
And as expected we are able to correctly identify the 4 clusters. As the Scikit-learn implementation initializes the starting centroids using kmeans++, the algorithm converges to the global minimum on almost every re-run of the training cycle.
Final Thoughts
K-means is the go-to unsupervised clustering algorithm that is easy to implement and trains in next to no time. As the model trains by minimizing the sum of distances between data points and their corresponding clusters, it is relatable to other machine learning models.
The code for this article can be found here.
Resources
- Pros and Cons of Kmeans — Google
- Kmeans Initialization Methods — Nitish Kumar Thakur
- Scikit-Learn Kmeans Documentation
- Elbow Method — Wikipedia
- Kmeans Clustering — Javatpoint
- StackEdit Markdown Editor
Unsupervised Learning: K-Means Clustering was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/6tWsLAR
via RiYo Analytics

ليست هناك تعليقات