https://ift.tt/cNrJom2 Practical Machine Learning Learn how to use this essential Machine Learning technique Image by author. This art...
Practical Machine Learning
Learn how to use this essential Machine Learning technique

This article will review one of the most important techniques in Machine Learning: nested cross-validation. When deploying a model, we select the best one from several choices (e.g., random forest vs. support vector machine) with the best combination of hyperparameters (e.g., random forest with 50 trees vs. one with 5 trees). However, we also need to estimate the generalization error (how well the model will do in production). Nested cross-validation allows us to find the best model and estimate its generalization error correctly.
At the end of the post, we provide a sample project developed with Ploomber that you can re-use with your data to get up and running with nested cross-validation in no time!
Why do we need cross-validation?
Let’s imagine we’re working on a Machine Learning project, and we have already done the heavy work of cleaning data and getting some training set, and we trained it. Are we ready to deploy it?
Not quite. Before deployment, we’d like to know how well the model will perform in production. To do so, we can compute an evaluation metric, let’s say accuracy.
Which data do we use to compute the metric? One way to do it would be to generate predictions for all observations in our training set and compute the evaluation metric:

This is how it looks in code:
Console output: (1/1):
Accuracy: 0.97
This approach is methodologically incorrect: we shouldn’t train and evaluate with the same data since our model already saw the training examples. Hence, it could simply memorize the labels and have perfect accuracy.
We split our data into two parts: training and testing to simulate production conditions (predicting on unseen data). With fit our model with the first part and evaluate with the second part.

Here’s how to do it with code:
Console output: (1/1):
Accuracy: 0.91
We can see that the estimate is lower this time (0.91 vs. 0.97); the higher estimate is an overly optimistic estimation of how our model will perform.
So this basic train/test approach is better than the first approach. Still, it has an issue: it’s sensible to the selection of the test set.
We could get lucky and select an easy test set causing an overly optimistic generalization error (or unlucky and have an overly pessimistic estimate). So to cover our ground, we can do the following: repeat the same process many times and average the results; this process is known as cross-validation:
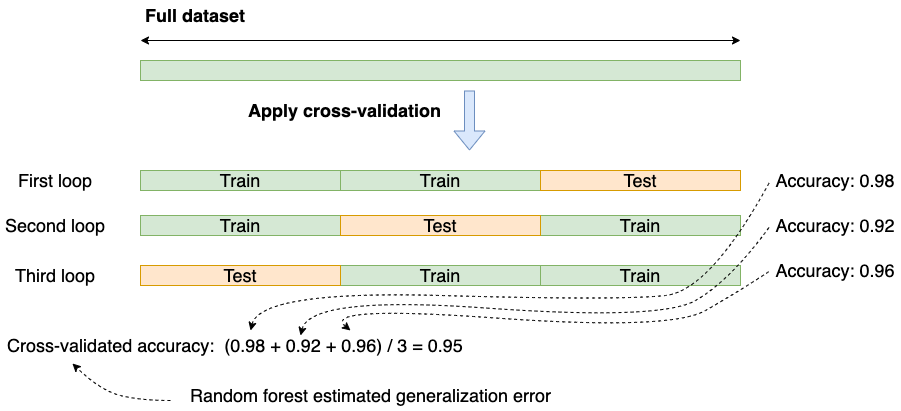
In summary: cross-validation provides us with a robust way to estimate the performance of our model in production.
Let’s implement it:
Console output: (1/1):
Cross-validated accuracy: (0.98 + 0.92 + 0.96) / 3 = 0.95
So now we got a result (0.95) that’s between the first (methodologically wrong) approach (0.97) and the second train/test approach (0.91).
Model selection
We have a way of estimating the generalization error with cross-validation, but we haven’t finished yet. Many models are available: random forest, XGBoost, support vector machines, logistic regression, etc. Since we don’t know which one will work best, we try a few of them.
So let’s say we try Random Forest and Support Vector Machine. We already have results for the Random Forest so let’s now run cross-validation on the Support Vector Machine.
Console output: (1/1):
Cross-validated accuracy: (0.96 + 0.98 + 0.94) / 3 = 0.96
Let’s summarize the results:
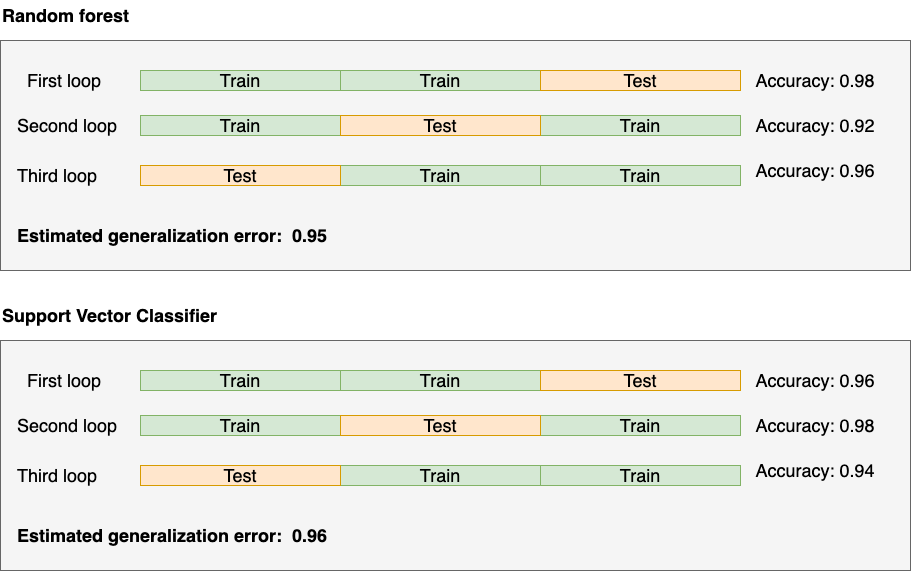
Based on the results, we should go with the Support Vector Machine.
However, we didn’t change the model’s parameters (for example, a random forest with a larger number of trees). So could it be that we made a sub-optimal decision?
Let’s try a few experiments, this time, train both models (using our cross-validation procedure) with a few hyperparameters:
Console output: (1/1):
SVC(kernel='linear', random_state=0):
Cross-validated accuracy: (1.00 + 1.00 + 0.98) / 3 = 0.99
SVC(kernel='poly', random_state=0):
Cross-validated accuracy: (0.98 + 0.94 + 0.98) / 3 = 0.97
RandomForestClassifier(n_estimators=2, random_state=0):
Cross-validated accuracy: (0.98 + 0.92 + 0.96) / 3 = 0.95
RandomForestClassifier(n_estimators=5, random_state=0):
Cross-validated accuracy: (0.98 + 0.94 + 0.94) / 3 = 0.95
Based on those results, we got an even better model! Support Vector Machine with a linear kernel with 0.99 accuracy!
Well, not quite. There’s a methodological mistake here.
We’re brute-forcing our way into finding the best model. This paper demonstrated that it’s possible to end up with an overly optimistic generalization error (due to overfitting) when we use the (vanilla) cross-validation method to optimize hyperparameters and model selection.
Enter nested cross-validation
We use nested cross-validation to fix the error described above, which provides a more accurate method for estimating the generalization error while also optimizing hyperparameters.
It gets its name since we are effectively nesting two cross-validation procedures. Let’s see how it looks in practice:
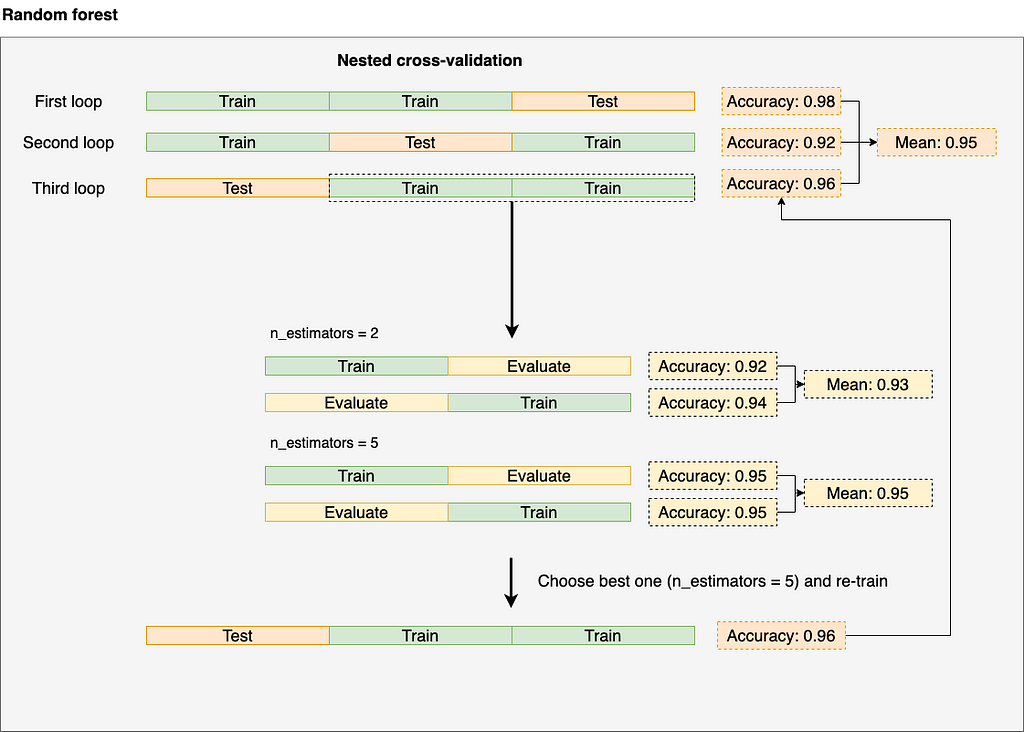
We are nesting two cross-validation loops. Look at the third one as a reference. We split again once we do the initial split (2/3 of our data). The inner loop optimizes hyperparameters: we train for each hyperparameter configuration (in this case, n_estimators = 2 and n_estimators = 5), compute the cross-validated metric (the mean) and pick the best hyperparameter configuration (in this case n_estimators = 5), then, we go to the outer loop and re-train using the best configuration ( n_estimators = 5) and report the accuracy. We repeat the same process until we finish.
By the end of the process, we’ll have a table that reports the estimated generalization error for each model; let’s run it:
Console output: (1/1):
GridSearchCV(estimator=RandomForestClassifier(random_state=0), param_grid={'n_estimators': [2, 5]}):
Cross-validated accuracy: (0.98 + 0.92 + 0.96) / 3 = 0.95
GridSearchCV(estimator=SVC(random_state=0), param_grid={'kernel': ['linear', 'poly']}):
Cross-validated accuracy: (1.00 + 0.94 + 0.98) / 3 = 0.97

We can confidently pick the Support Vector Machine as our winner model with this information. We can also say that it has an estimated generalization error of 0.97 (look that this is lower than our previous estimate of 0.99 where we didn’t use nested cross-validation).
As a final step, we run a final cross-validation procedure to find the optimal parameters. Note this is a vanilla cross-validation process:
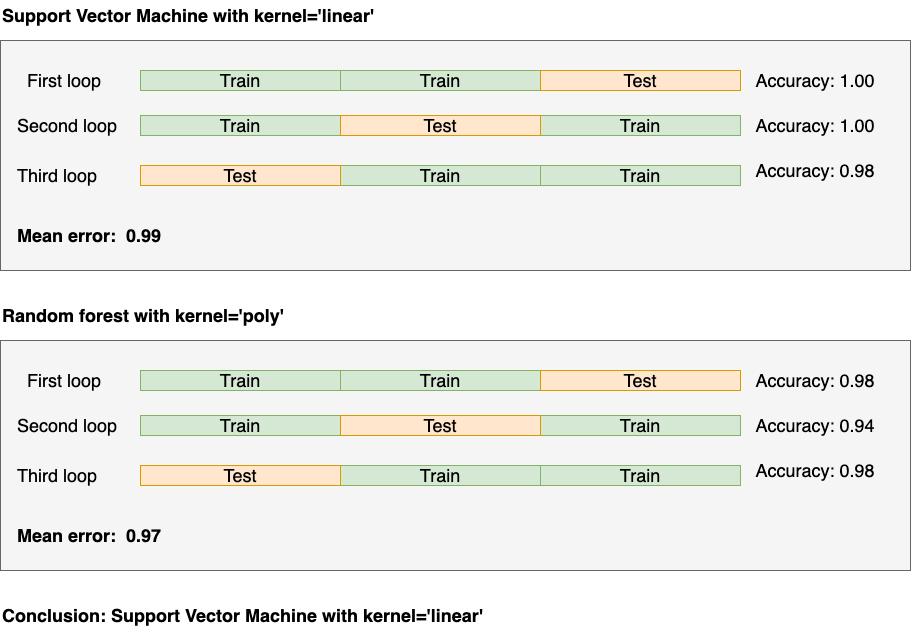
Here’s the code:
Console output: (1/1):
SVC(kernel='linear', random_state=0):
Cross-validated accuracy: (1.00 + 1.00 + 0.98) / 3 = 0.99
SVC(kernel='poly', random_state=0):
Cross-validated accuracy: (0.98 + 0.94 + 0.98) / 3 = 0.97
So now we’re ready to deploy: we’ll deploy the Support Vector Machine with kernel = 'linear'!
But consider a crucial point: we’ll report 0.97 (via the nested cross-validation procedure) as our generalization estimate, not the 0.99 we got here.
That’s it! You are now equipped with the nested cross-validation technique, to select the best model and optimize hyperparameters!
Sample code
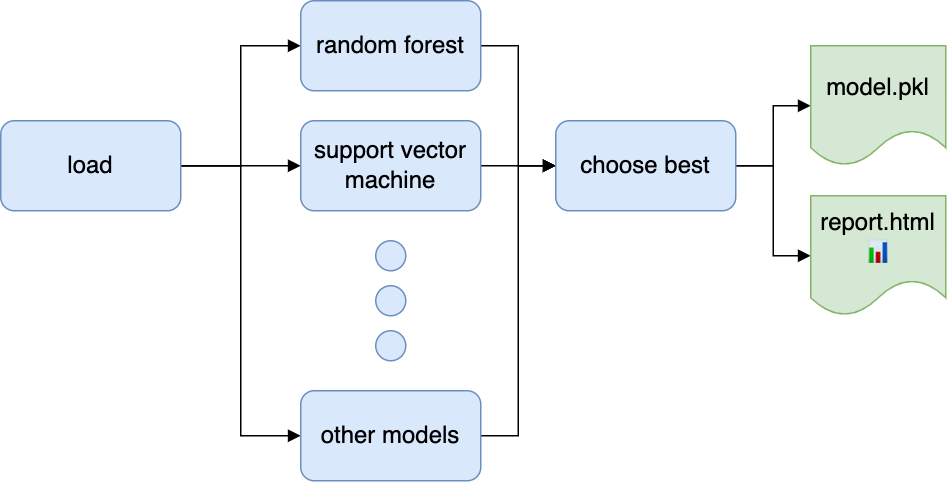
For your convenience, we’ve put together a sample Ploomber pipeline to get you up to speed; here’s how to get it:
Once you execute the pipeline, check out the output/report.html file, which will contain the results of the nested cross-validation procedure. Edit the tasks/load.py to load your dataset, run ploomber build again, and you'll be good to go! You may edit the pipeline.yaml to add more models and train them in parallel.
Caveats
In our example, we only evaluated two models with two configurations. However, since we’re nesting two cross-validation processes, the number of training procedures snowballs. If we add a few more models and hyperparameters, we’ll soon be required to run hundreds of training procedures to find the best model. So, to speed up results, you might want to run all those experiments in parallel; you can easily do it with Ploomber in one machine. Still, if you want to distribute work across multiple machines, you’ll have to set up some cloud infrastructure. Alternatively, you can try Ploomber Cloud, which will quickly start the necessary resources, execute your code in the cloud (and parallelize jobs), get you the results, and shut down the infrastructure, so you don’t keep those expensive servers running. All without leaving your notebook.
Final thoughts
During my days as a data scientist, it took me some time to fully grasp the concept of nested cross-validation. So I hope this post helps you. Do you have any questions? Reach out to our community, and we’ll be happy to help.
Originally published at ploomber.io
Model Selection Done Right: A Gentle Introduction to Nested Cross-Validation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/i6TaQrL
via RiYo Analytics

No comments