https://ift.tt/ey8silQ Photo by Arthur V. Ratz Everything That Readers Need To Know About Bidirectional Associative Memory (BAM), With S...

Everything That Readers Need To Know About Bidirectional Associative Memory (BAM), With Samples In Python 3.8 and NumPy
Introduction
Bidirectional Associative Memory (BAM) is a recurrent neural network (RNN) of a special type, initially proposed by Bart Kosko, in the early 1980s, attempting to overcome several known drawbacks of the auto-associative Hopfield network, and ANNs, that learn associations of data from continuous training.
The BAM is the hetero-associative memory, providing an ability to store the associated data, regardless of its type and structure, without continuous learning. The associations of data are simultaneously stored, only once, prior to recalling them from the BAM’s memory. Normally, the BAM outruns the existing ANNs, providing significantly better performance while recalling the associations. Also, using the BAM perfectly solves the known bitwise XOR problem, compared to the existing ANNs, which makes it possible to store the data, encoded to binary (bipolar) form, in its memory.
Unlike the unidirectional Hopfield network, the BAM is capable of recalling the associations for data, assigned to its either inputs or outputs, bidirectionally. Also, it allows retrieving the correct associations for even incomplete or distorted input data.
The BAM models are rather efficient when deployed as a part of an AI-based decision-making process, inferring the solution to a specific data analysis problem, based on various associations of many interrelated data.
Generally, the BAM model can be used for a vast of applications, such as:
- Classification and clustering data
- Incomplete data augmentation
- Recovering damaged or corrupted data
The BAM models are very useful whenever the varieties of knowledge, acquired by the ANNs, are not enough for processing the data, introduced to an AI for analysis.
For example, the prediction of words missed out from incomplete texts with ANN, basically requires that the associations of words-to-sentences are stored in the ANN’s memory. However, this would incur an incorrect prediction, because the same missing words might occur in more than one incomplete sentence. In this case, using the BAM provides an ability to store and recall all possible associations of the data entities, such as words-to-sentences, sentences-to-words, words-to-words, and sentences-to-sentences, and vice versa. This, in turn, notably increases the quality of prediction. Associating various entities of data multi-directionally is also recommended for either augmenting or clustering these data.
Finally, the memory capacity of each ANN’s layer is bound to the size of the largest floating-point type: float64. For instance, the capacity of a single ANN layer of shape (100x100) is only 1024 bytes. Obviously, the number of the ANN’s layers, as well as the number of neurons, in each of its layers, must be increased to have the ability to store the associations and recall them multi-directionally. This, in turn, negatively impacts the ANN-based memory latency, since its learning and prediction workloads are growing, proportionally to the sizes of the ANN.
Despite this, the high performance of learning and prediction of the BAM provides an ability to allocate as large amounts of memory space as required, beyond the conventional ANN’s memory capacity limits. As well, it’s possible to aggregate multiple BAMs into the memory, having a layered structure.
Associations Stored In Memory…
The BAM learns the associations of various data, converted to bipolar patterns. A bipolar pattern is a special case of binary vector, the elements of which are the values of 1's and -1's, respectively. Multiple patterns (columns) are arranged into the 2D-pattern maps, along the y-axis of a matrix.x The pattern maps are the embeddings, each column of which corresponds to a specific input and output data item, stored in the BAM’s memory:
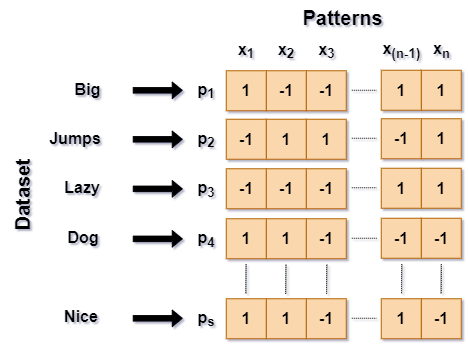
The BAM model simultaneously learns the associated data from pattern maps, assigned to its corresponding inputs and outputs, respectively:
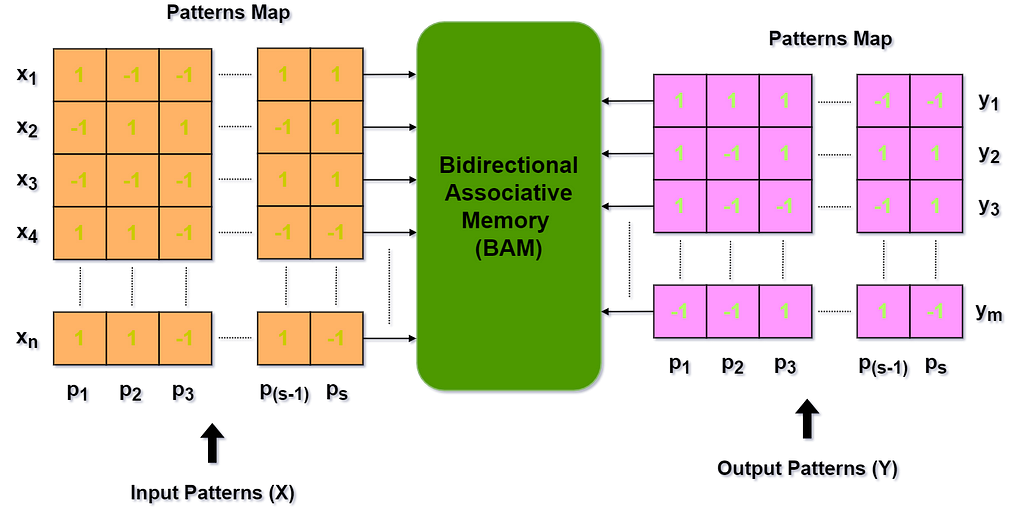
In the figure, above, the BAM model learns the associations of data, encoded into the pattern maps 𝙓 and 𝒀 of the shapes (𝙨 x 𝙣) and (𝙨 x 𝙢), respectively. While learning, the values from the input and output patterns are assigned to the corresponding inputs 𝙭ᵢ ∈𝙓 and outputs 𝙮ⱼ∈ 𝒀 of the BAM’s model. In turn, both input and output pattern maps (columns) must have an equal number of patterns (𝙨 ). Since the BAM is a hetero-associative memory model, it has a different number of inputs (𝙣 ) and outputs (𝙢 ), and, thus, the different number of rows in those pattern maps, 𝙓, and 𝒀, correspondingly.
BAM’s Topology And Structure
Generally, the BAM is a primitive neural network (NN), consisting of only input and output layers, interconnected by the synaptic weights:
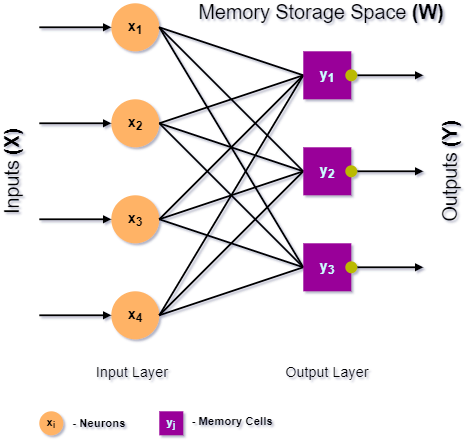
In the figure, above, the neurons (𝒏) of the input layer perform no output computation, feedforwarding the inputs 𝑿 to the memory cells (𝒎) in the BAM’s output layer. Its sizes basically depend on the quantities of inputs and outputs of the BAM (e.g., the dimensions of the input and output pattern maps). The NN, shown above, of the shape (4 x 3), consists of 4 neurons and 3 memory cells in its input and output layers, respectively.
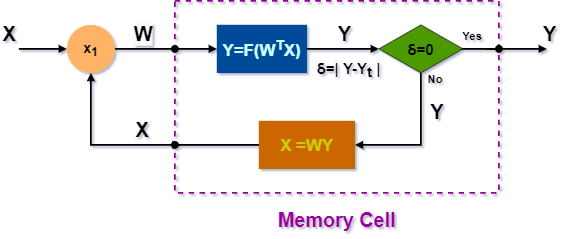
Unlike the conventional ANNs, the output layer of BAM consists of memory cells that perform the BAM’s outputs computation. Each memory cell computes its output 𝒀, based on the multiple inputs 𝑿, forwarded to the cell by the synaptic weights 𝑾, each one is of specific strength.
The outputs of memory cells correspond to specific values of patterns, being recalled:
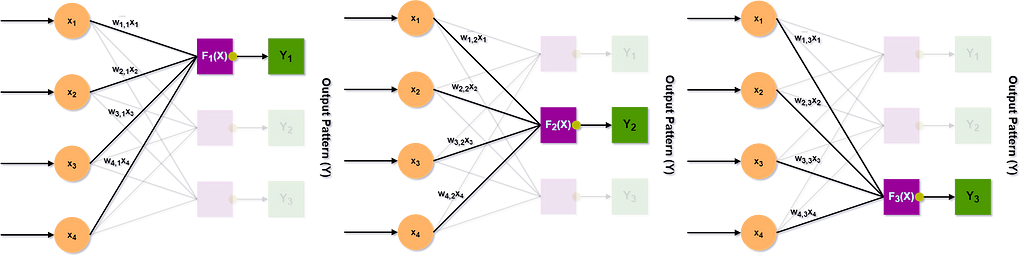
The BAM’s outputs are computed as the weighted sum of all BAM’s inputs 𝑾ᵀ𝙓, applied as an argument to the bipolar threshold function. The positive (+) or negative (-) value (e.g., 1 or -1) of each output 𝒀 is always proportional to the magnitude of the sum of the cell’s weighted inputs.
All synaptic weights, interconnecting the input neurons and memory cells store the fundamental memories, learned by the BAM, based on the Hebbian supervised learning algorithm, discussed, below.
Learning Algorithm
Algebraically, the ability of BAMs to store and recall associations solely relies on the bidirectional property of matrices, studied by T. Kohonen and J. Anderson, in the mids of 1950s:
The inner dot product of two matrices 𝑿 and 𝒀, which gives a correlation matrix 𝑾 is said to be bidirectionally stable, as the result of recollection and feedback of 𝑿 and 𝒀 into 𝑾 .
Generally, it means that the corresponding rows and columns of both matrices 𝑿 and 𝒀, as well as their scalar vector products, equally contribute to the values of 𝑾, as the recollections:
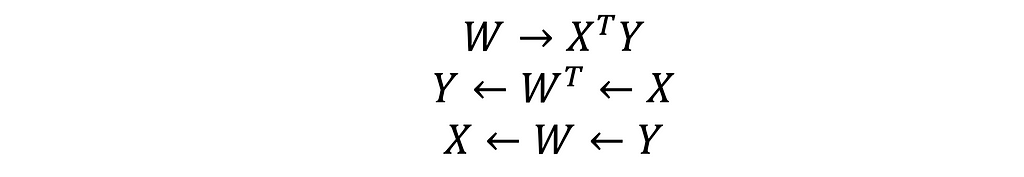
Since that, each vector of the matrices 𝑿 and 𝒀 can be easily recalled by taking an inner dot product 𝑾𝑿ₖ or 𝑾 𝒀ₖ, discussed, below.
In this case, 𝑾 is a matrix, which infers the correlation of the 𝑿ₖ or 𝒀ₖ vectors. An entire learning process is much similar to keeping (𝙬ᵢⱼ≠ 0) or discarding (𝙬ᵢⱼ=0) the specific weights, that interconnect input neurons and memory cells of the BAM.
The values of synaptic weights 𝙬ᵢⱼ∈ 𝑾 can be either greater than, less, or equal to 0. The BAM keeps only those synaptic weights, which values are either positive or negative. The synaptic weights, equal to 0, are simply discarded while initializing the model.
The bidirectional matrix property was formulated by Donald Hebb as the famous supervised learning rule, which is fundamental for the Hopfield network, and other associative memory models.
According to the Hebbian algorithm, all associated patterns are stored in the BAM’s memory space, only once, while initializing the matrix 𝑾ₙₓₘ of the synaptic weights (e.g., memory storage space). The matrix 𝑾ₙₓₘ is obtained by taking an inner dot product of the input 𝑿ₚₓₙ and output 𝒀ₚₓₘ pattern maps (i.e., matrices), respectively:
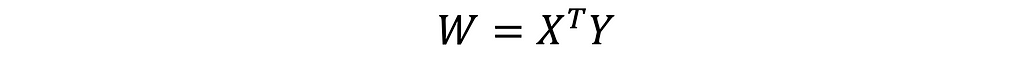
Alternatively, the weights matrix 𝑾ₙₓₘ can be obtained as the sum of outer Kronecker products of the corresponding patterns 𝙭ₖ and 𝙮ₖ, from the 𝑿ₚₓₙ , 𝒀ₚₓₘ matrices.
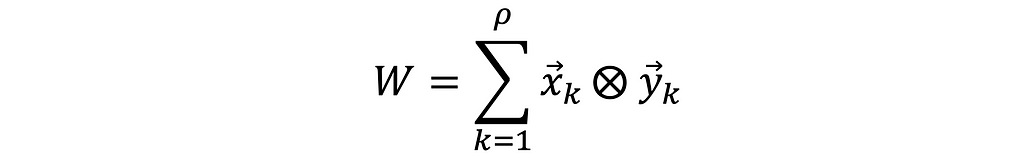
Unlike the inner dot product of 𝑿 and 𝒀, the outer products of (𝙭ₖ,𝙮ₖ) ∈ 𝑿,𝒀 vectors yield matrices 𝙬ₖ ∈ 𝑾 (i.e., the fundamental memories). Finally, all of the matrices 𝙬ₖ are combined into a single matrix 𝑾, by obtaining their sum, pointwise.
An entire process of the BAM’s synaptic weights intialization is illustrated in the figure, below:

However, the correlation matrix 𝑾 provides the most stable and consistent memory storage, for the patterns, which are the orthogonal vectors. The product of orthogonal vectors in 𝑿,𝒀 gives the symmetric correlation matrix 𝑾, in which the fundamental memories of associations, learned from the pattern maps 𝑿 and 𝒀, respectively.
Thus, it’s highly recommended to perform the orthogonalization of 𝑿 and 𝒀 pattern maps, prior to training the model. Since the 𝑿 and 𝒀 are bipolar, the orthogonalization of 𝒀 can be easily done as: 𝒀 = -𝑿. By taking the negative -𝑿, the 𝒀 patterns will have the same values as 𝑿, the sign (+/-) of which is changed to an opposite.
The BAM’s learning algorithm is trivial and can be easily implemented as 1-line code, in Python 3.8 and NumPy:
Recalling Patterns From The Memory
Since the input and output pattern maps have been already stored in the BAM’s memory, the associations for specific patterns are recalled by computing the BAM’s full output, within a number of iterations, until the correct association for an input pattern 𝑿 was retrieved.
To compute the full memory output, in each of the iterations 𝞭-iterations, 𝒌=𝟏..𝞭, the BAM’s inputs 𝙭ᵢ of the pattern 𝙓 are multiplied by the corresponding synaptic weights 𝙬ᵢⱼ∈ 𝙒. Algebraically, this is done by taking an inner product of the weights matrix 𝙒-transpose and the input pattern 𝙓. Then, the weighted sum 𝙒 ᵀ𝙓 of the BAM’s inputs is applied to the bipolar threshold function 𝒀=𝙁(𝙒 ᵀ𝙓), to compute each memory cell’s output, which corresponds to a specific value 1 or -1, of the output pattern 𝙮ⱼ∈ 𝒀, being recalled. This computation is similar to feedforwarding the inputs through each layer of the conventional ANN.
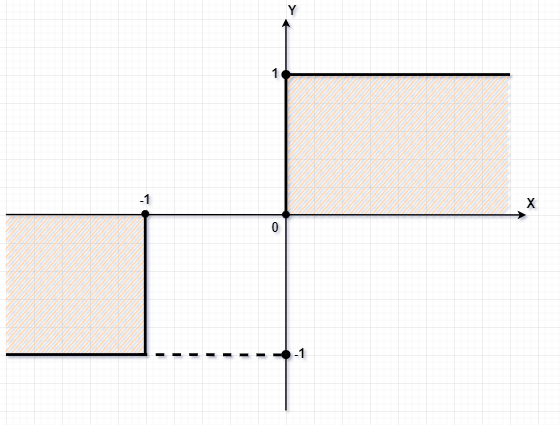
The bipolar threshold function 𝙁 is just the same as the classical threshold function with only a difference that its value for the positive (+) or 0 inputs is 1, and negative (-), unless otherwise. In this case, the positive input of 𝙁 also includes zero:
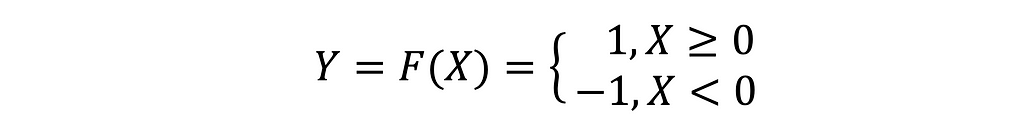
The bipolar threshold function’s plot diagram is shown, below:
A simple fragment of the code, demonstrating the BAM’s memory cells activation is listed below:
Unlike the conventional ANNs, the memory cells in the output layer also compute the new inputs 𝙓ₖ₊₁ for the next iteration 𝙠+𝟏. Then, it performs a check on whether the current 𝙓 and new inputs 𝙓ₖ₊₁ are not equal (𝙓≠𝙓ₖ₊₁). If not, it assigns the new inputs to the BAM, proceeding to compute the output 𝒀 in the next iteration. Otherwise, if 𝙓=𝙓ₖ₊₁, then it means that the output 𝒀 is the correct association for the input 𝙓 , and the algorithm has converged, returning the pattern 𝒀 from the procedure. Also, the BAM provides an ability to recall the associations for either inputs 𝙓 and outputs 𝒀, by computing the memory outputs, bidirectionally, based on the same algorithm, being discussed.
The patterns recalling process is illustrated in the figure, below:
An algorithm for recalling the association from the BAM’s memory is listed below:
Let 𝑾ₙₓₘ— the correlation weights matrix (i.e., the BAM memory storage space), 𝑿ₙ— an input pattern of the length 𝒏, 𝒀ₘ— an output pattern of the length 𝒎:
Recall an association 𝒀 for an input pattern 𝑿, previously stored in the BAM’s memory:
For each of the 𝞭-iterations,𝟏 ≤ 𝞭 ≤ 𝒕, do the following:
- Initialize the BAM’s inputs with the input vector 𝑿₁←𝑿.
- Compute the BAM output vector 𝒀ₖ , as an inner dot product of the weights matrix 𝑾 ᵀ transpose, and the input vector 𝑿ₖ, for the 𝒌-th iteration:
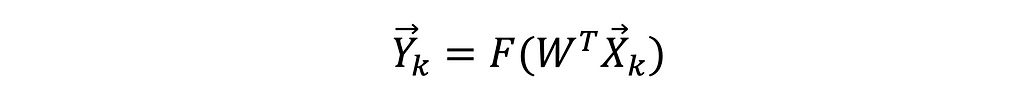
3. Obtain the new input vector 𝑿ₖ₊₁ for the next (𝒌+𝟏)-th iteration, such as:
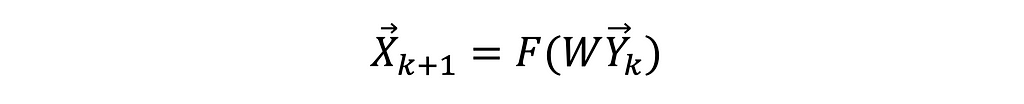
4. Check if new and existing vectors 𝑿ₖ₊₁≠𝑿ₖ, are NOT the same:
If not, return to step 1, to compute the output 𝒀ₖ₊₁, for the (𝒌+𝟏)-th iteration, or proceed to the next step 5, unless otherwise.
5. Return the output vector 𝒀←𝒀ₖ from the procedure, as the correct association for the input 𝑿 vector.
6. Proceed with steps 2–4, until convergence.
A fragment of code in Python 3.8 and NumPy, implementing the patterns prediction algorithm is listed, below:
Memory Evaluation (Testing)
The code, listed below, demonstrates the BAM evaluation (testing) process. It builds the BAM model of a specific shape (patterns×neurons×memory_cells), and generates 1D-array, consisting of the 1 and -1 values. Then, it reshapes the array into the input 2D-patterns map 𝑿. To obtain the patterns map 𝒀, it performs the orthogonalization of 𝑿, such as: 𝒀=−𝑿. Next, the correlation matrix is computed to store the associations of patterns in 𝑿 and 𝒀 into the BAM’s memory.
Finally, it performs the model evaluation for each input pattern 𝙭ᵢ ∈ 𝙓 it recalls an association from the BAM’s memory, bidirectionally. When an association y⃗ₚ for the input pattern x⃗ was recalled from the memory, it does the consistency check whether the output y⃗ₚ target y⃗ pattern are identical, displaying the results for each of the input patterns 𝙭ᵢ ∈ 𝙓:
Predicting Incomplete Patterns
One of the BAM model’s advantages is an ability to predict the correct associations for by >30 incomplete or damaged inputs. The fragment of code, below, demonstrates the incomplete patterns prediction. It randomly selects an input pattern from the patterns map 𝑿, and distors it, replacing its multiple values with an arbitrary 1 or -1. It applies the poison(…) function, implemented in the code, below, to distort the randomly selected pattern x⃗ , the association for which is being recalled. Finally, it predicts an associated pattern, performing the consistency check if the target and predicted associations, y⃗ and y⃗ₚ are identical. If so, the correct association for the distorted pattern x⃗ has been recalled:
Conclusion
Despite its agility to store and recall the associations without continuous learning, the BAM model might become less efficient for some applications, due to the inability to recall the correct associations for data of certain types. According to the latest research, predicting associations for various incomplete or corrupted data basically requires the BAMs of enormously huge sizes, consisting of large amounts of memory cells. There are also several issues while recalling the correct associations for a small number of patterns, being stored. Obviously, the existing variations of the BAM models must undergo improvements to be used as persistent memory storage, for a vast of applications. Although, the workarounds to the following issues are still in process.
Source Code:
- “Bidirectional Associative Memory (BAM) In Python 3.8 And NumPy”, Jupyter Notebook @ Google Colab
- Bidirectional Associative Memory, Python 3.8 + NumPy Samples, Visual Studio 2022 Project @ GitHub Repository
Disclaimer
All images were designed by the author of this story, by using the Draw.io application, https://www.diagrams.net/
References
- “Bidirectional associative memory” — From Wikipedia, the free encyclopedia.
- Adaptive bidirectional associative memories, Bart Kosko, IEEE Transactions on Systems, MAN, And Cybernetics, VOL.18, No. 1, January/February 1988.
- Pattern Association or Associative Networks, Jugal Kalita University of Colorado at Colorado Springs.
A Succinct Guide To Bidirectional Associative Memory (BAM) was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/ru2CgRp
via RiYo Analytics

No comments