https://ift.tt/L9zv854 Understand these concepts to improve your impact Photo by Jens Lelie on Unsplash Are you familiar with random ...
Understand these concepts to improve your impact

Are you familiar with random forests, the bias-variance tradeoff, and k-fold cross-validation? If you are a professional data scientist, you probably are.
You have likely spent countless hours learning various techniques for building high-performance predictive models. This is no surprise given the abundance of online content devoted to the tools we use to solve problems.
Much less content explores the concepts we need to identify the right problems to solve. This article outlines three of these concepts.
3. Cogency vs. verisimilitude
Fundamentally, what is the goal of a model? In most data science applications, the goal is to provide information that supports a decision. When a model excels at this goal, it exhibits cogency. The problem is that we often lose sight of cogency in the pursuit of verisimilitude, the property of a model that depicts reality in detail. Let’s consider an example.
Imagine that a business faces an important decision that depends on the total number of user purchases next month, so they ask two data scientists to provide forecasts.
Jim, the first data scientist, builds a relatively simple time-series forecasting model that focuses on historical monthly purchase counts. His model accounts for recent trends, seasonality, and several macro-level variables that drive the variance in monthly purchase counts.
Dwight, the second data scientist, wants to build a better model than Jim’s. He believes that Jim’s model is too coarse and fails to account for detailed user-level dynamics. Dwight spends two weeks building a complicated model that predicts whether each user will purchase each product available next month. Once Dwight finishes his model, he aggregates the user-level predictions into a final number — the estimated total number of purchases for next month.
Dwight’s model is more detailed than Jim’s, but is it better?
Probably not.
The issue is that Dwight has lost sight of the decision at hand in an effort to paint a detailed picture of reality.
There are several reasons why Jim’s model is superior to Dwight’s:
- Jim’s model is much cheaper to build and maintain.
- Dwight’s model is harder to explain to the decision-makers, making it less likely to be impactful.
- Jim’s model will probably be more accurate because it is optimized to predict the quantity of interest directly. The errors in Dwight’s user-level predictions can accumulate into significant errors at the macro-level.
Jim’s model is focused on cogency, while Dwight’s model is focused on verisimilitude.
The distinction between cogency and verisimilitude comes from Ronald Howard’s book, “The Foundations of Decision Analysis Revisited [1].” In this, he writes:
Is verisimilitude the criterion for decision models? Is a decision model that includes “the sales tax in Delaware” better than one that does not? The answer is no, unless that factor is material to the decision. The criterion for decision models is cogency: whether the model leads to crisp clarity of action for the decision maker. You should eliminate any feature that does not contribute to this goal.
A more detailed model is not necessarily a better one. If you’re trying to decide whether to pack a sweater, you don’t worry about intermolecular dynamics in the atmosphere.
How much detail should we include in a model? The next two concepts help answer this question.
2. The “rule of one-fourth” in uncertainty propagation
Too often, we worry about reducing uncertainties that do not practically matter. They don’t matter because larger uncertainties dominate the decisions.
Let’s consider an example. A data scientist is tasked with predicting the average spending for new users on a platform. They quickly build a simple linear regression model with a prediction accuracy of +/- 5%.
This model is not a bad starting point, but the data scientist believes they can do better. They invest the next week into experimenting with different models and hyperparameters. They eventually settle on a well-crafted ensemble of models with an impressive accuracy of +/- 1%.
The data scientist gives the model to the stakeholders, and the conversation goes something like this:
Stakeholders: “Wow, it’s incredible that you were able to cut the prediction error from 5% to 1%. That’s an 80% reduction in error!”
Data scientist: “Thank you. Out of curiosity, what will the model be used for?”
Stakeholders: “We will use your model to forecast total revenue from new users. We have projections for the number of installs. Your model predicts the average spending of new users. If we multiply your model’s predictions by our projected install counts, we will estimate the total revenue from new users.”
Data scientist: “What is the uncertainty of the install count projections”
Stakeholders: “About +/- 20%”
In this case, the stakeholders actually care about the total revenue from new users:
Total revenue = (average revenue per install) x (# of installs)
The uncertainty in the quantity of interest results from two uncertainty contributions — the contribution from uncertainty in the data scientist’s model and the contribution uncertainty in the install count projections.
Because the equation is linear, the relative uncertainty contributions are equal to the individual relative uncertainties. So, the uncertainty contribution from the data scientist’s model is 1%, and the uncertainty contribution from the install count projections is 20%. In other words, if there were only uncertainty from the model, the overall uncertainty would be 1%. If there were only uncertainty from the install count projections, the overall uncertainty would be 20%.
The way uncertainty contributions combine is somewhat surprising. Intuitively, one might think that uncertainty contributions add. This is not true. The math more closely resembles the Pythagorean theorem; the squares of the uncertainty contributions add. This arises from the fact that variances add rather than standard deviations. Please see the Wikipedia page on the propagation of uncertainty for more details on the math.
The mathematics of uncertainty propagation amplify the impact of large uncertainty contributions relative to small ones.
If we assume that the errors from the model are uncorrelated with those from the projection, the uncertainty in the total revenue is actually sqrt(0.01² + 0.2²) = 20.0% (with rounding).
If the data scientist had instead used the simple regression model with an uncertainty of 5%, the overall uncertainty would be sqrt(0.05² + 0.2²) = 20.6%. They also would have saved a week of their time.
Was it worth the data scientist’s time to reduce the overall uncertainty from 20.6% to 20%? Probably not.
In this case, the dominant uncertainty contribution was only four times larger than the smaller uncertainty contribution.
When working on a project, ask yourself the following:
- What is the quantity we care about for decision-making?
- What is the dominant source of uncertainty in the quantity we care about?
As a rule of thumb, avoid investing excessive time and resources into modeling a component whose uncertainty contribution is smaller than one-fourth of the dominant uncertainty contribution.
Even if you magically model the component with perfect accuracy, you will reduce the overall uncertainty by less than 3%. More often than not, the improvement will be totally insignificant to the decisions you support.
A data scientist should focus on the dominant uncertainty if possible. Imagine if the data scientist had instead focused the week of their time improving the install count projection. If they had reduced the uncertainty from 20% to 18%, the overall uncertainty would be sqrt(0.05² + 0.18²)=18.7%. Reducing an uncertainty from 20% to 18% sounds a lot less impressive than reducing an uncertainty from 5% to 1%, but the impact is greater in this case.
1. Value of information
In my opinion, this is the single most underrated concept in data science.
From Wikipedia, the value of information (VoI) is “is the amount a decision-maker would be willing to pay for information prior to making a decision.”
For professional data scientists, the decision-maker is usually a company or a client.
VoI is incredibly important because it shows data scientists how to quantify the value of what they do. In fact, VoI is the actual figure of merit we care about when modeling. In most cases, performance metrics such as mean squared error and classifier accuracy are proxies to VoI. We generally assume that a more performant model is a more valuable one. This assumption is valid if the increased performance potentially leads to different actions.
To understand VoI, we must think about the difference in value between a situation with information and without information. We often hear the ubiquitous buzzwords “data-driven decision-making.” Ever think about the difference in value between a data-driven decision and an “ordinary” decision? This is what VoI is all about.
Once again, let’s consider an example. A company has a successful pizza delivery website. They are considering expanding their website to include a hamburger delivery feature. The company has done preliminary market research into whether this feature would be successful, but they think a data scientist might uncover additional insights to clarify the decision.
Before hiring the data scientist, the company is optimistic that the burger delivery feature will succeed. For simplicity, let’s say that a simple distribution with two outcomes well describes their prior beliefs:
- A 75% chance that the new feature will succeed and make $8 million.
- A 25% chance that the new feature will fail and cost $2 million.
The company could make this decision without hiring a data scientist. In this case, the decision situation is depicted with the following tree:
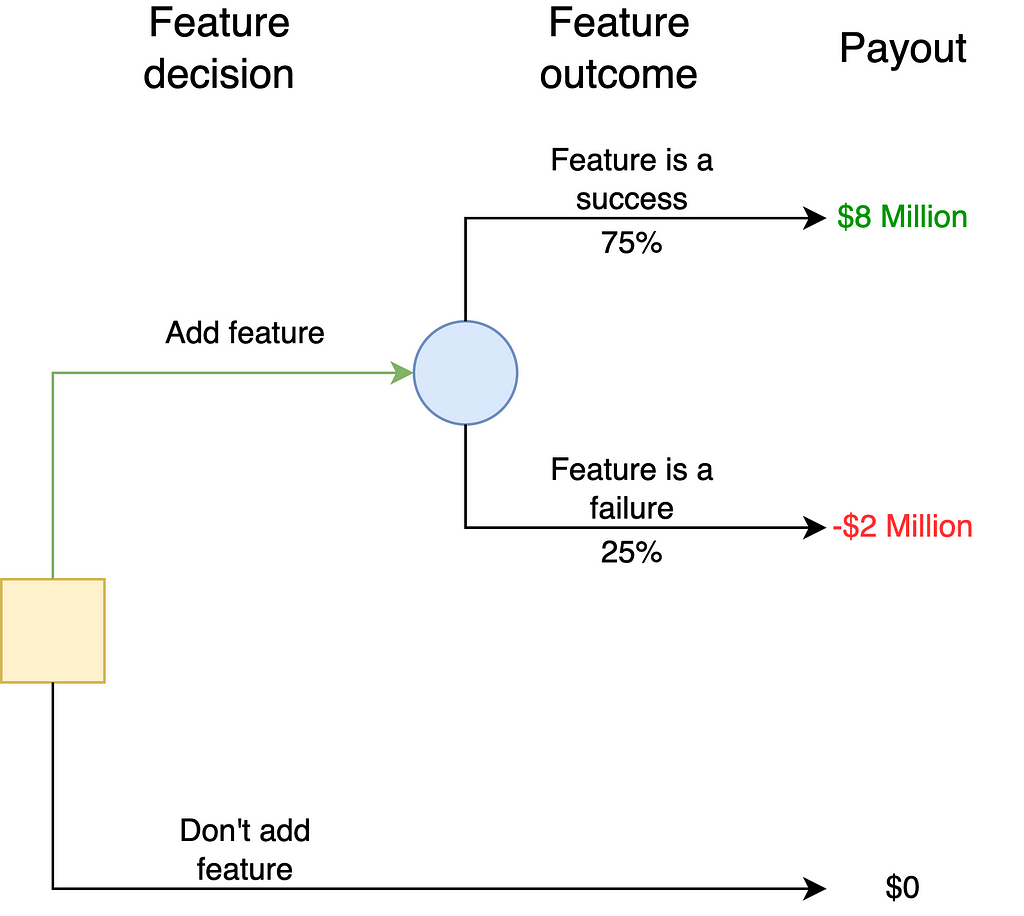
If the company is risk-neutral, it will launch the feature. The expected value of the feature is (0.75 x $8 million)-(0.25 x $2 million) = $5.5 million, which is greater than $0.
Still, the company believes it might be worth hiring a data scientist. Conveniently, an applicant named Claire submits her resume to the company. Claire is well-versed in a new machine learning algorithm that issues predictions by tearing open the space-time continuum to see directly into the future. Claire has the unique ability to create a perfectly accurate model for a price. How much should the company pay Claire for her gifts?
To answer this question, consider how Claire’s model would change the decision tree:
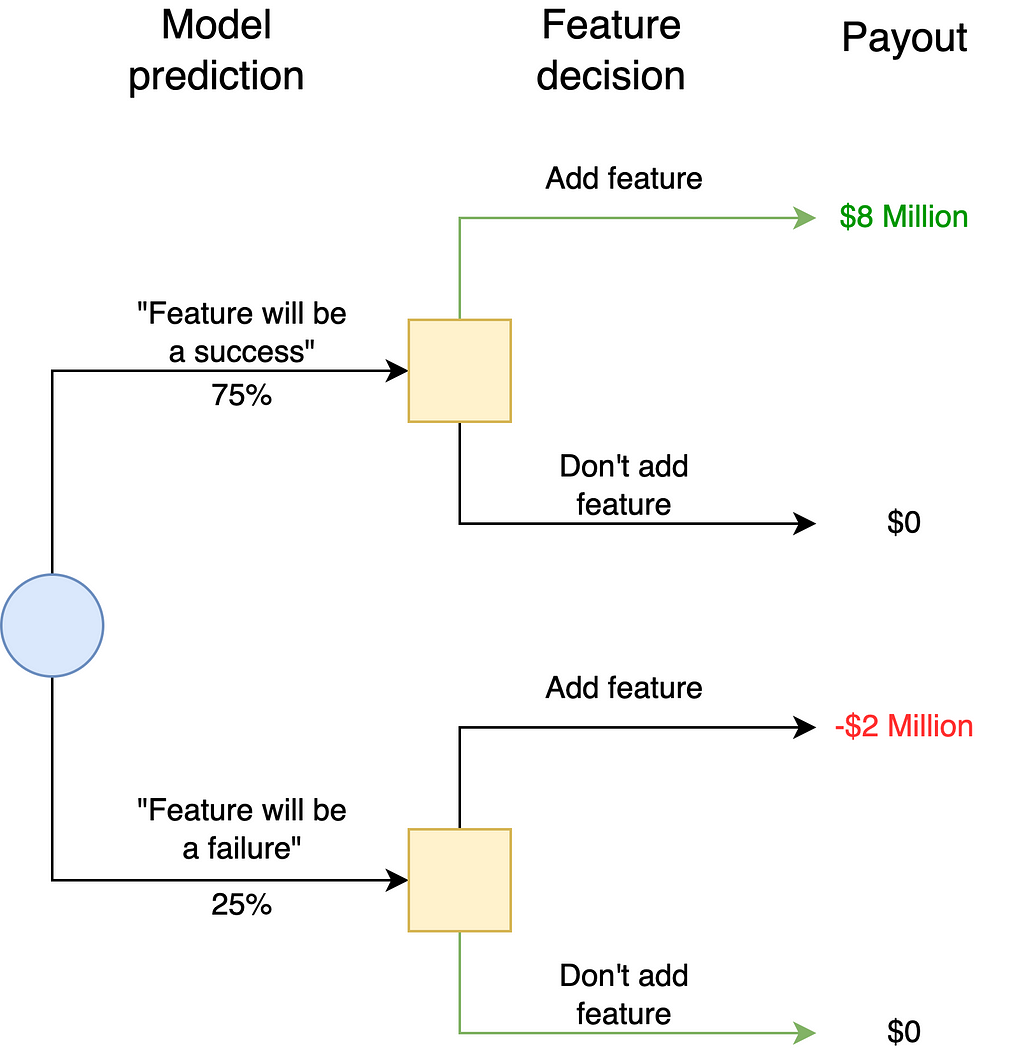
The key modification is that the company will now know whether the feature is a success or a failure before they decide to launch it. There is uncertainty because the company does not know what Claire will predict.
However, once Claire provides her prediction, there is no longer uncertainty. There is a 75% chance that she predicts the feature’s success. In this case, the company would launch the product and earn $8 million.
There is a 25% chance that she predicts the feature’s failure. In this case, the company would not launch the product, incurring $0. Compare this situation to the previous tree in which the company would launch the feature unconditionally and potentially incur the $2 million cost of a failed launch.
Claire’s model has value because it might predict the feature’s failure. The company could cancel the feature’s launch in response to her prediction. Her model’s prediction is actionable.
In order for information to be valuable, it must have the potential to change action.
To calculate VoI, we must determine the value of the decision situation with free information (ignoring the cost of Claire’s services). This value is (0.75 x $8 million)-(0.25 x $0 million) = $6 million. Claire’s perfect model improves the value of the decision situation by $500,000, so its VoI is $500,000.
In reality, none of us are as skilled as Claire; our models have errors. The VoI for a perfect model is known as the value of clairvoyance (VoC). VoC is helpful because it establishes an upper bound for the value of a data science effort.
A data scientist should never invest more than the value of clairvoyance into solving a problem.
Calculating VoI is harder than calculating VoC because it must account for our models’ imperfections. The details of the VoI calculation accounting for modeling error are outside the scope of this article. I highly recommend Eric Bickel’s webinar on the topic to learn more. For a discussion on calculating VoI for A/B tests, I recommend this blog post.
To understand the impact of a question, data scientists should have a sense of the value of clairvoyance. If your business could pay a clairvoyant to answer the question you’re trying to answer with 100% certainty, how much would it pay?
Final remarks
Thank you for taking the time to read this post. I hope you find these concepts helpful in your data science journey.
References
- Howard, R.A. , 2007. The Foundations of Decision Analysis Revisited. In: Edwards, W., Ralph, J., Miles, F. and Winterfeldt, D.v. (Editors), Advances in Decision Analysis. Cambridge University Press, New York, NY, pp. 32–56.t
Three of the Most Underrated Data Science Concepts was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/wo7lS6n
via RiYo Analytics

ليست هناك تعليقات