https://ift.tt/caikmEN Funky Programming in Python “Snap out of the loop” Freaking Vortex by Nicholaus Gurewitch. Source on the left of ...
Funky Programming in Python
“Snap out of the loop”

If you skipped your CS classes dealing with tree traversals or you can’t understand how to extract the shortest route from A to B using Dijkstra’s algorithm, you might’ve googled your way to recursions. I’ll assume you’ve read what there is to read on the top 2 search results.
So, I’ll try to explain with my own words how to approach recursions with ease, and why you perhaps shouldn’t to that. Afterwards we’ll have some fractal fun.
Dark side of the Loop
To get a running start, we can imagine a recursion as a loop. Or we can imagine the loop as a recursion. Either way, they share some similarities.
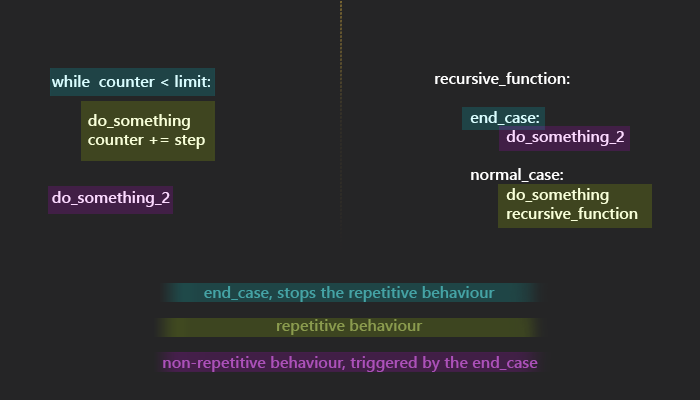
Obviously, some actions are being taken repeatedly until a condition is met. There is a condition which stops the repetition and there are actions which follow.
Recursive functions generally call upon themselves as part of their repetitive actions, regular loops don’t sport that kind of behavior. Still, many regular loops can be written as recursions, as I will gladly demonstrate:
The Humble Iteration
To successfully make a simple recursive function, I’ll follow this skeleton:
recursive_function:
end_case:
do something before ending
end
normal_case:
do something before calling the function again
recursive_function
Now, say we wanted to repeat a certain action X times. The for-loop flows naturally in place:
for i in range(X):
repeated_action
And the recursive function, following the aforementioned skeleton:
def recursive_iteration(X, counter=0):
#end_case:
if counter == X-1:
return
#normal_case:
repeated_action
recursive_iteration(X, counter+1)
Not so slick… And wait until we start adding utility to it…
The Sum
Let’s say we want the sum of all integers from 0 to X.
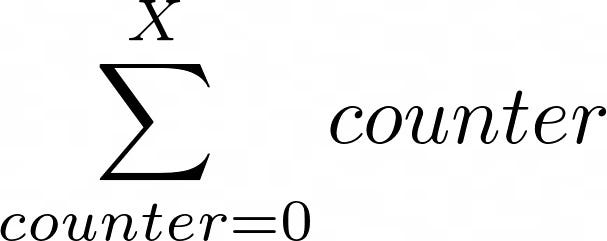
The Admirable For-Loop:
sum = 0
for counter in range(1,X+1):
sum+=counter
And the Atrrocious Recursion:
def recursive_sum(X, counter=1):
#end_case:
if counter == X:
return counter
#normal_case:
return counter + recursive_iteration(X, counter+1)
Break it down
If you haven’t exactly managed to comprehend what’s happening in the code above, here’s a step-by-step visual aid which I hope will suffice:
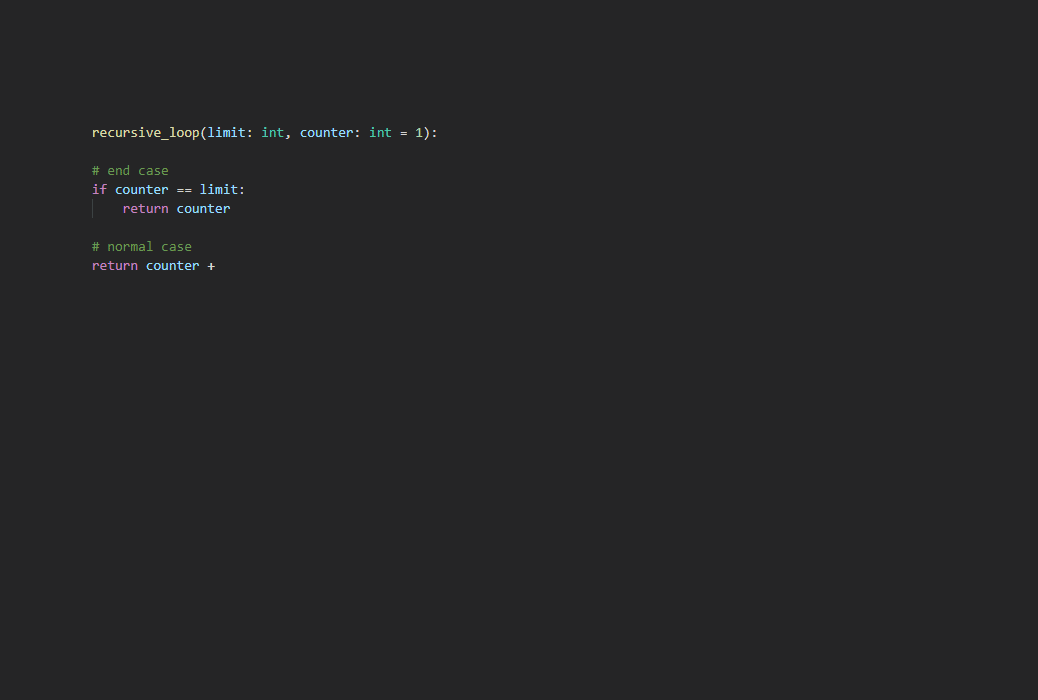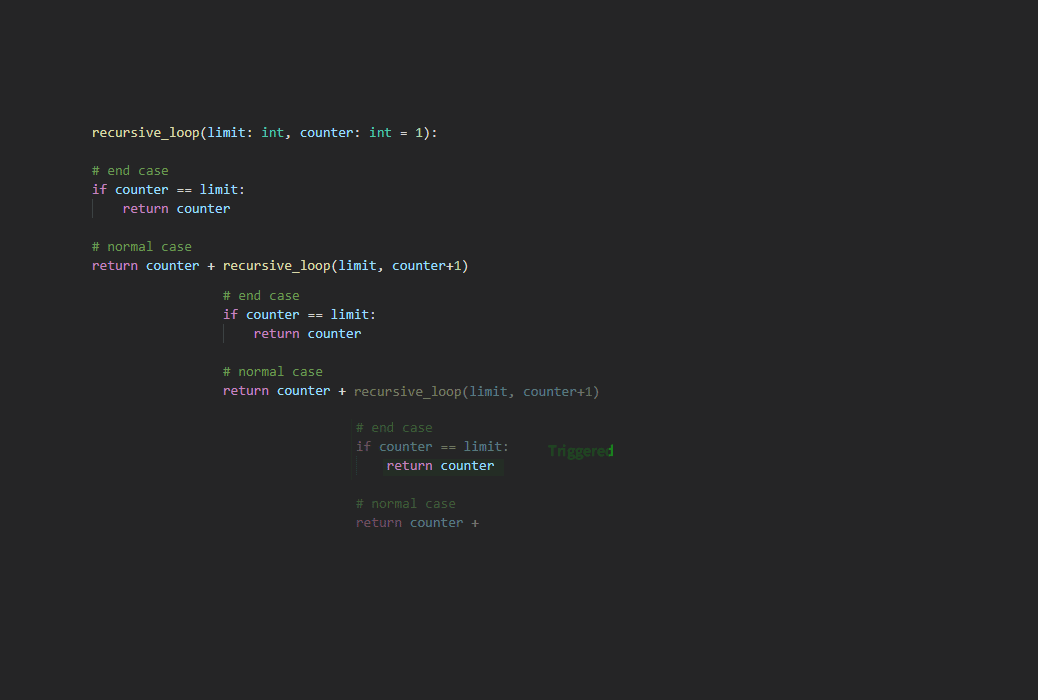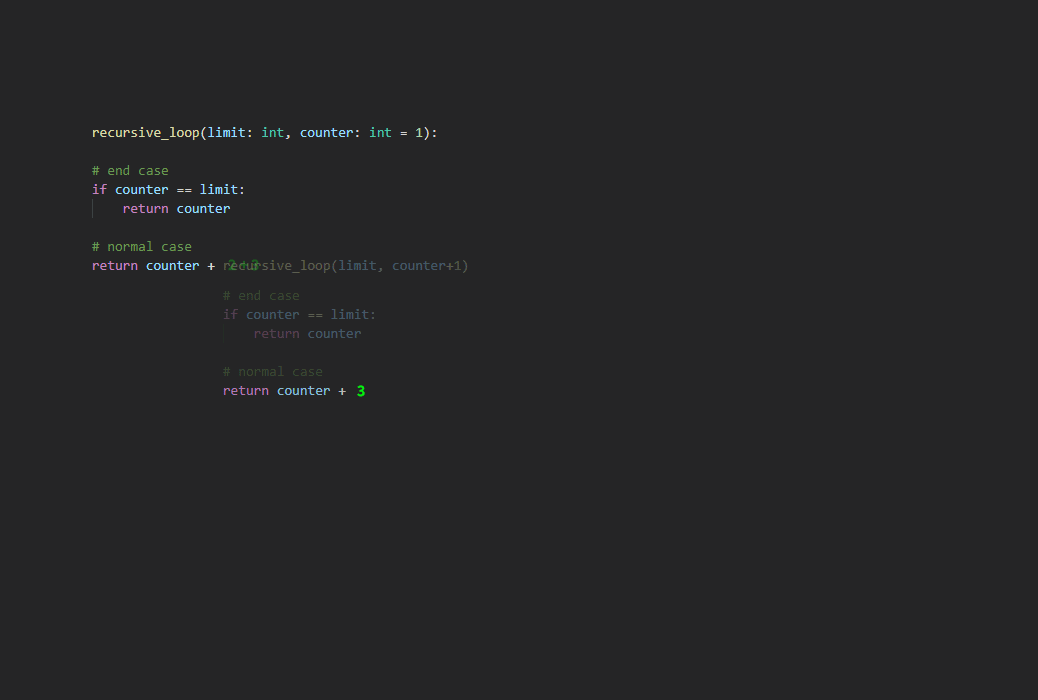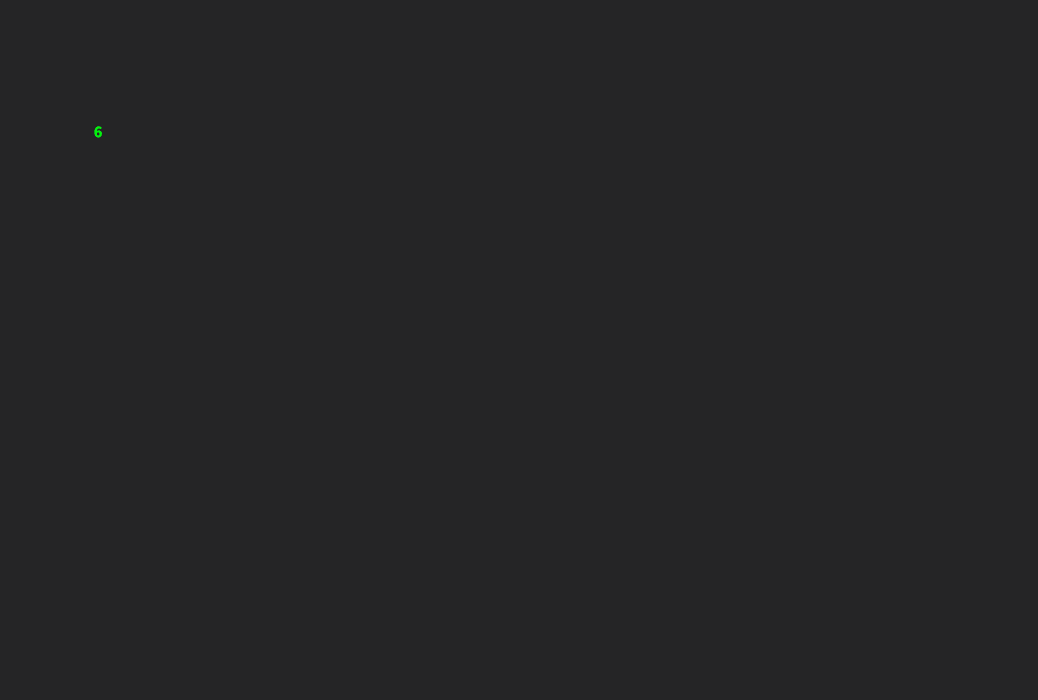
Whoops, seems like I’ve made the animation with some different names…
Recursions or Loops?
If you have a clear choice between the two, choose loops.
Alongside the eyesore and brain-pain sometimes associated with using recursions, another considerable downside is the overhead. Make a recursion and a loop that do the same task and time them to reveal the problem
Recursion Use-Case
The real fun begins when regular loops aren’t fit for the job, that’s the domain of the recursion. Where loops complicate and fail, the recursion reigns.
Once you can wrap your mind around the recursive process, you need to develop a sense for using them properly. I recognize the need for recursions when I start thinking things like “this should be repeated but zoomed in every step”. Now, I’m not going to show you anything useful, instead I promised fractal fun at the beginning of the article, so let’s get to it.
Fractal Funtime
If you endow in philosophic discourse (or arguing with strangers over the internet) or introspection, you might have noticed some recursive thought patterns emerge. It can seem that recursions are woven into the human brain. Some examples from nature imply that beauty stems from geometrical regularity and recursions are no exception, although in nature they mostly come in the form of fractals.
To make this article geometrically appealing, let’s try to solve a graphical recursion assignment.
The Five
First off, let me introduce the Five.
Five is a 2D array, noted as [[1,0,1],[0,1,0],[1,0,1]]
Why is it a called “the Five”? If you visualize 1 as a white px, and 0 as a black px, it looks somewhat like a 5 from a dice (I guess it’s possible someone reading this has never seen a dice…)

[0,1,0]
[1,0,1]
[image, by, author]
This COULD easily be hardcoded, but let us not indulge in such behavior…
five = []
for i in range(3):
row = []
for j in range(3):
# This is a method for generating checkerboard patterns, makes sure that the rows change the order of 1’s and 0's
if (j+i)%2 == 0:
row.append(1)
else:
row.append(0)
five.append(row)
Ok, so now we have defined and coded the Five. Onto the next step…
Five made out of Fives
The next concept to grasp is; what if instead of 1’s we use Fives, and instead of zeros use 3x3 Zero Matrices?

There are obvious easy ways to reach this shape, but I hope you can extrapolate where this is going… Because no amount of hardcoding can help you there.
The …Five made out of (Five made out of (Five made out of (Five made out of Fives)))
My friends call me Fractal Five

Let’s think of a strategy.
The problem can be approached with the help of a recursion skeleton I typed out way above.
In our normal case, we want the function to do the shape of the Five, but with different strides every level of recursion it takes.
For example, the first iteration takes into scope the entire image (2D matrix), and splits it into 3x3 blocks. To do that, it strides 1/3 of the scope width and height.
Each block is taken into the second iteration, and defines the scope of that iteration. The stride remains 1/3 of the scope, and the block is further split into 3x3 blocks.
The process repeats in a recursive fashion, as it should.
The process needs to stop sometime, so we introduce an end case.
In this example, the end case is when the scope is 3x3 pixels. Obviously, going a layer deeper would mean going into sub-pixel territory and my mom always said never to go there. Instead, when we reach the 3x3 px scope (and a stride of 1), we’ll just draw the Five.
To make it work, we need to pass the matrix, scope and current x and y coordinates (to know where to draw the white px) to the function as arguments.
def rec(mat,scope,x,y):
stride = scope/3
#### End Case ################
if stride == 1/3: # DO NOT go into the sub-pixel territory...
x,y = int(x),int(y)
mat[y,x] = 255 # Paint it white
return
##### Normal Case ############
remember_x = x
for i in range(3):
for j in range(3):
if (j+i)%2 == 0:
rec(mat,stride,x,y) # Call the function again
x+= stride
y+= stride
x = remember_x
# The loops can be done as "in range(0,3*stride,stride)
# But this seemed more readable to me at the time
# When all recursions are done, return the matrix for viewing
if scope == mat.shape[0]:
return mat
To make the function more user friendly, I’ve wrapped it into another function
def fractal_five(number_of_iterations):
dim = 3**number_of_iterations
mat = rec(np.zeros((dim,dim)),dim,0,0)
return mat
This way, the function can be called with a single argument, and produce a square 2d matrix filled with Fractal Fives. Importing numpy as np and using it’s ndarrays makes it easy to visualize the result in opencv later on.
When rethinking the process, it seems the other way around could work out quite a lot faster. Starting with 3x3 pixels and recursively working our way towards the full scope of image, but I think that’s enough of this article. The recursive thought process isn’t only computationally expensive for the computer, but for your brain too. Be sure to snap out and enjoy the regular, linear stream of thought.
Disclaimer: Feel free to use all the content with the tag [image/animation by author]
Recurring Concerns Concerning Recursions was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/iEcSj5A
via RiYo Analytics

No comments