https://ift.tt/oS4Vex7 Background In a world where NFT’s are being sold for millions, the next profitable business might be to create uniq...
Background
In a world where NFT’s are being sold for millions, the next profitable business might be to create unique virtual entities and who better suited for the job than artificial intelligence. In fact, well before the NFT hype, in October 2018, the first AI-generated portrait was sold for $432,500. Since then, people have used their deep knowledge of advanced algorithms to make astounding pieces of art. Refik Anadol, for instance, is an artist who uses AI to create captivating paintings. (I urge you to check some of his work at this link). Another digital artist, Petros Vrellis, put up an interactive animation of Van Gogh’s celebrated artwork “Starry Night” in 2012, which reached over 1.5 million views within three months. AI’s creative capabilities aren’t limited to artwork though. People are building intelligent systems that can write poems, songs, story-plots, and possibly do other creative jobs as well. Are we moving towards a world where all artists will be competing against AI? Perhaps, however, that’s not what I intend to discuss. My aim with this post is to dive into the working of an elegant algorithm, Neural Style Transfer, that might help abysmal painters like me become art virtuosos.
1. Neural Style Transfer-The idea
Any image can be divided into two constituents, content and style. Content refers to the intricacies of different objects, while style is the overall theme. You can also interpret the two as local and global entities of an image. For instance, in the image below, the detailed design of the Eiffel tower is the content whereas, the background shades — blue sky and green surroundings — constitute the style (theme).

The idea of Neural Style Transfer(NST) is to take one image and recompose its content in the style of some other image. Unlike the above case, transferring themes(style) from more appealing pictures, like the famous starry night painting by Van Gogh, can result in fascinating recompositions.

Let’s discuss the above transformation in detail.
2.CNNs for style transfer
Since we are dealing with images, it shouldn’t surprise you that convolutional neural networks are at the crux of style transfer. Also, because ample CNNs have achieved incredible results in image processing tasks, we don’t need to train a separate one for NST. I’ll use the vgg-19 network(transfer learning for style transfer), but you can use any other pre-trained network or train your own.
The Vgg-19 network has the following architecture:
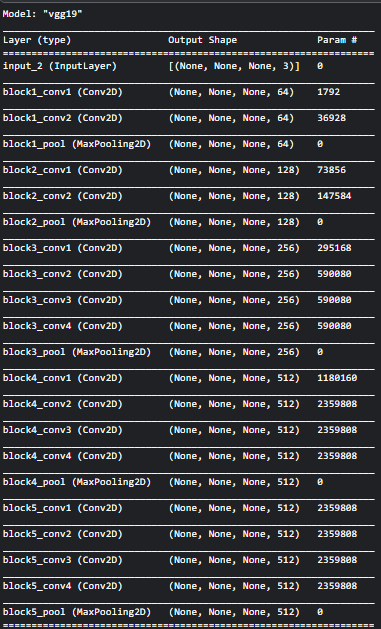
First, let’s see what some of the above layers lear recognize. Each layer has at least 64 filters to learn image features. For simplicity, we’ll use outputs from the first ten filters to see what these layers learn. If you want the code, you can use either of the following links.
NeuralStyleTransfer_experiments
https://github.com/shashank14k/MyWork/blob/main/neuralstyletransfer-experiments.ipynb
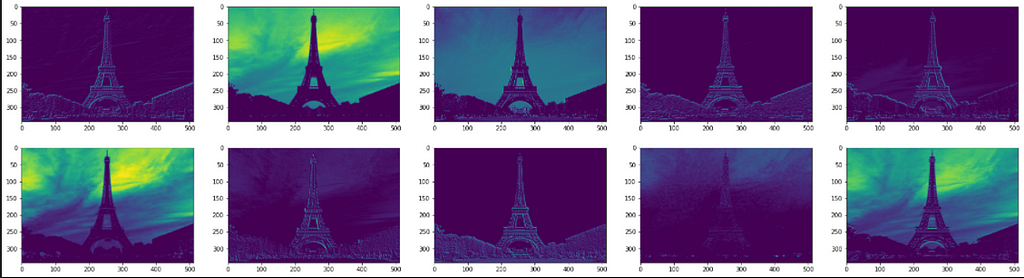
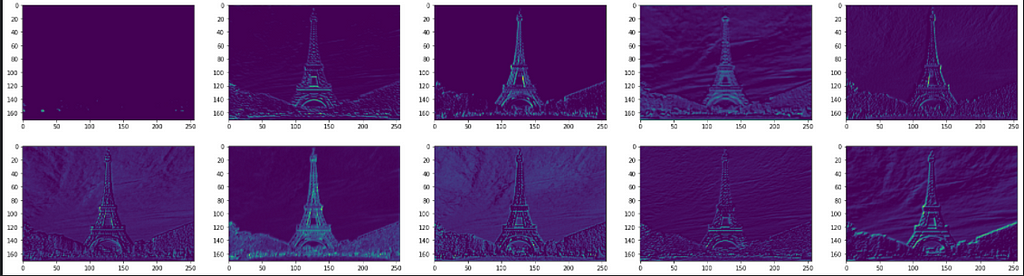
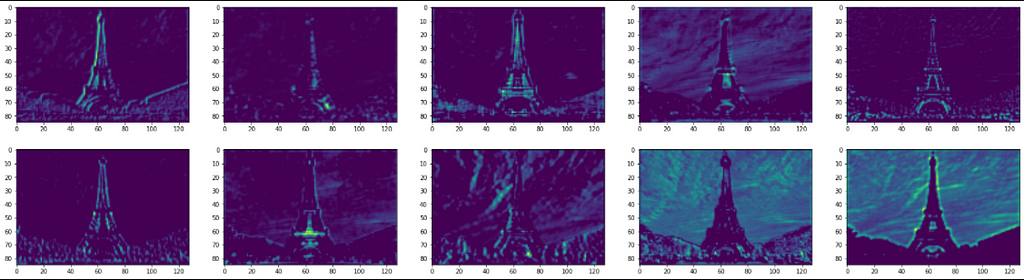
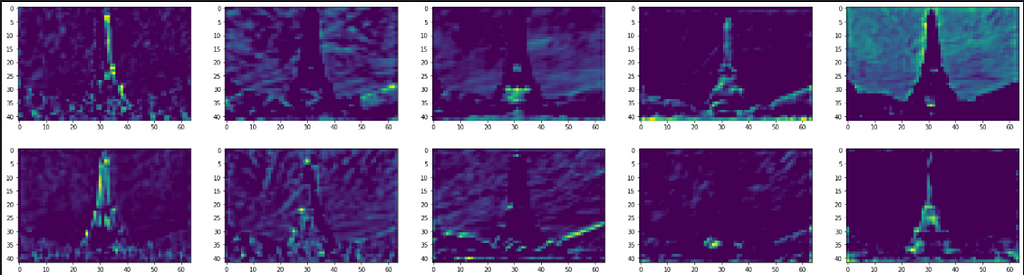
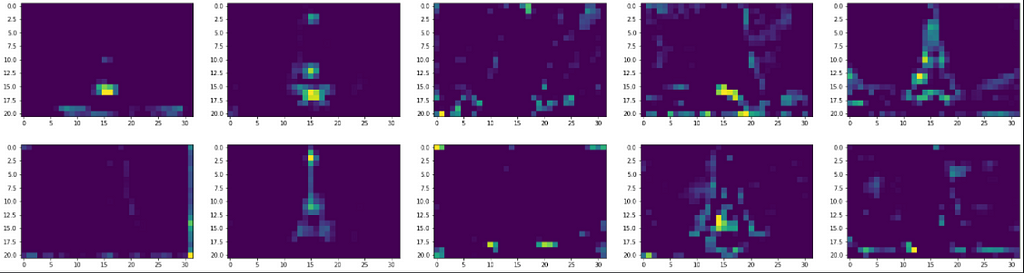
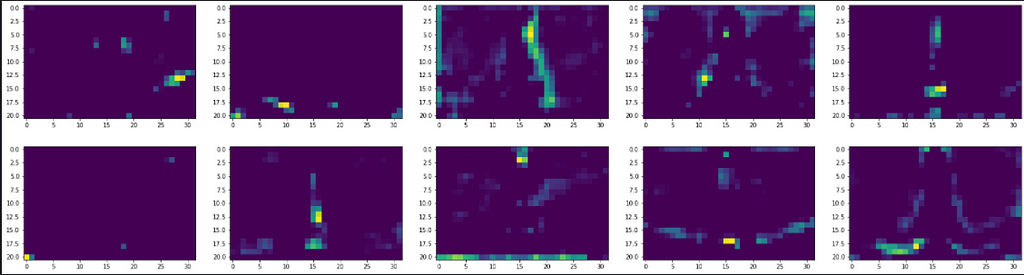
What do you make from the above plots? The initial layers seem to identify the overall context of the image (global attributes). These layers appear to recognize edges and colors globally, and hence their outputs closely replicate the original image. It is akin to tracing a photograph with butter paper. You may not reproduce the intricacies of distinct objects in the photo, however, you get an accurate overall representation.
Then, as the image progresses through the network, the outputs distort. Filter outputs in these layers, especially block_5_conv_2, are focused on specific locations and pull information about the shapes of different objects. The two filters below, for example, are interested in the finer details of the Eiffel tower. In a classification problem, perhaps, these local features will help CNNs distinguish the Eiffel tower from any other building of a similar outline like electric towers.
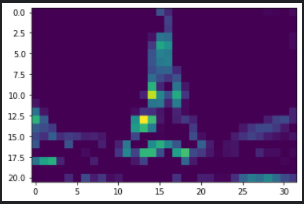
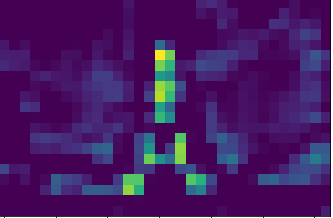
This separability of global and local constituents of an image using CNNs is what drives style transfer. Authors of a neural algorithm of artistic style, the original paper on neural style transfer(Gatys et al), report that since the deeper layers perform well at identifying detailed features, they are used for capturing image content. Similarly, the initial layers, capable of forging a good image outline, are used to capture image style(theme/global attributes).
3. Image Recomposition
Our aim is to create a new image that captures content from one image and style from another. First, let’s address the content part.
3.1 Content Information
We established in the previous section that outputs from a deeper layer help identify image content. We now require a mechanism to capture the content. For that, we use some familiar mathematics — loss functions and backpropagation.

Consider the above noise image(X). Also, for simplicity, assume our choice of CNN for style transfer consists of only two layers, A1 and A2. Passing the target image (Y) through the network and using A2’s outputs, A2(A1(Y)), we obtain information about its contents. To learn/capture this information, we pass X through the same network. As X consists of randomly arranged pixel values, A2(A1(X)) is also random. We then define a content loss function as:

Here, (i,j) are index notations for locations in the image array. (Size of target content image and noise image must be equal). Essentially, if the resulting arrays A2(A1(X)) and A2(A1(Y)) are of shape (m,n), the loss function computes their difference at each location, squares them, and then sums them up. With this, we force X to be an image, that when passed through the network, produces the same content information as Y. We can then minimize the content loss using backpropagation like we usually do in any neural network. However, there’s a minor difference. In this case, the values of image array X, instead of network weights, are the variables. Hence the final equation is:
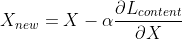
We can extend this idea to a network of any size and chose any suitable layer to gather content information.
3.2 Style Information
Capturing style is more complex than capturing content. It requires understanding gram matrices.
3.2.1 Gram Matrices
If you refer to the architecture of vgg-19 (section 2), you’ll see that the output of block_1_conv_1 is of shape (m,n,64). For simplicity assume that m,n = 3,2 and the number of filters are also 2 instead of 64.
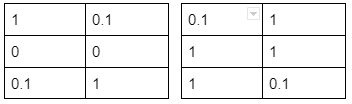
As you know, CNN filters learn to identify varying attributes-spatial features like edges/lines, color intensity, etc. Let’s say the above filters recognize shades of red and blue at different locations. Hence, the pixel value (ranging 0–1) at each index in filter 1’s output represents the intensity of color red at that location. Filter 2 gives the same information about the color blue. Now, stack the two output arrays, and take a dot product of the resulting array with its transpose. What do we get?

The final result is a correlation matrix of the attributes identified by the two filters. If you examine the outputs of the two filters, you’ll note that locations with high red intensity have less blue flavor. Hence the non-diagonal value of the dot product matrix (correlation between red and blue) is less. If we now alter pixel values such that red and blue appear together, the non-diagonal value will increase.

Ergo, a gram matrix, in the context of CNNs, is a correlation matrix of all features identified by all filters of a layer. Let’s see how they help in style transfer.
3.2.2 Style and combined loss

Suppose we wish to transfer style from the above image. Note the presence of multiple streaks (vertical and horizontal lines) of light blue(tending to white) color. Gram matrix of two filters that identify lines and light blue color will return a high correlation between these features. Consequently, the algorithm will ensure that these features appear together in the recomposed image and do a good job of transferring style. In reality, each CNN layer has numerous filters, which results in bulky gram matrices, but the idea remains valid. Gram matrix of block_1_conv_1’s output in vgg-19, for example, will be a correlation matrix of 64 features.
Next, we need to establish the function for style loss. Suppose, upon passing the target style image through block_1_conv_1 we get a gram matrix G. We input our noise image X through the same layer and compute its gram matrix (P). The style loss is then calculated as:

Here,(i,j) are index notations for locations in the gram matrices. By minimizing this function, we ensure that X has the same feature correlations as our target-style image.
Another thing to note is that, unlike content loss which was calculated from a single layer, style loss is calculated from multiple layers. Gatys et al used five layers for this purpose. Hence the final style loss is:

W is the weight assigned to loss from each layer. It’s a hyperparameter and can be tweaked around to see how the recomposition changes. We’ll discuss the result of altering these weights and using a single layer for style transfer in the last section.
The combined loss function is the sum of style and content loss. Again, each individual function has a weight. More weight to style will ensure that the recomposed image captures more style and vice versa.
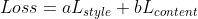
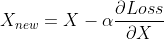
4. Changing the hyperparameters
Finally, with the theory discussed, let’s experiment neural style transfer with different hyperparameters. You can refer to the notebook links provided above for code. For your reference, the style transfer function is called with the arguments:
- Path of content image
- List of paths of style images
- Content loss weight
- Style loss weight
- Number of iterations (backpropagation)
- List of weights for the style images — In case you want to transfer style from multiple images, you’ll need to provide weight to each target style image
- List of weights for style layers — The weights assigned to each layer involved in the style loss function
We’ll use the following images for carrying out the experiments:

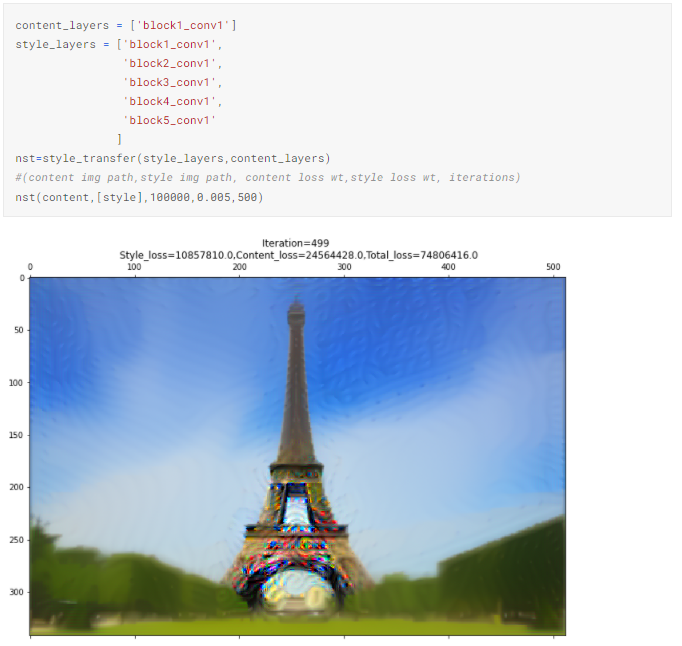
4.1 5 style layers with equal loss weights, 1 content layer
We’ll use this image to compare the result of altering the hyperparameters.
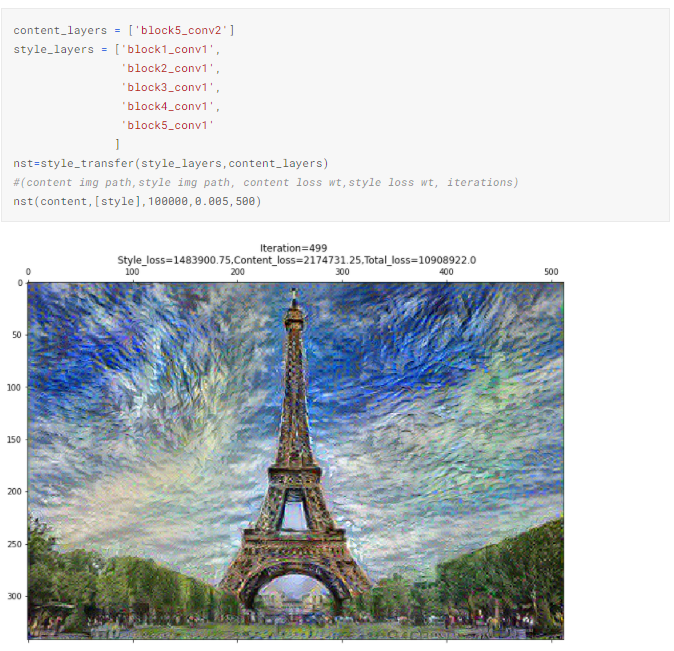
4.2 Increasing weight of style loss function from 0.005 to 0.1
As expected, increasing the weight nudges the algorithm to capture more style. Hence, the recomposition has a better combination of blue and yellow.
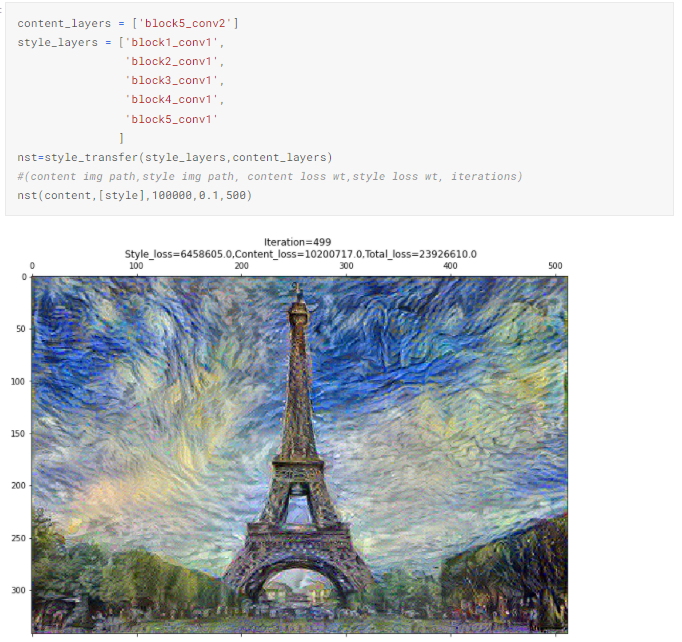
4.3 Using a single layer for style
Using just block_1_conv_1 for style loss does not result in a captivating recomposition. Perhaps, as syle consists of various shades and spatial attributes, filters from multiple layers are necessary.
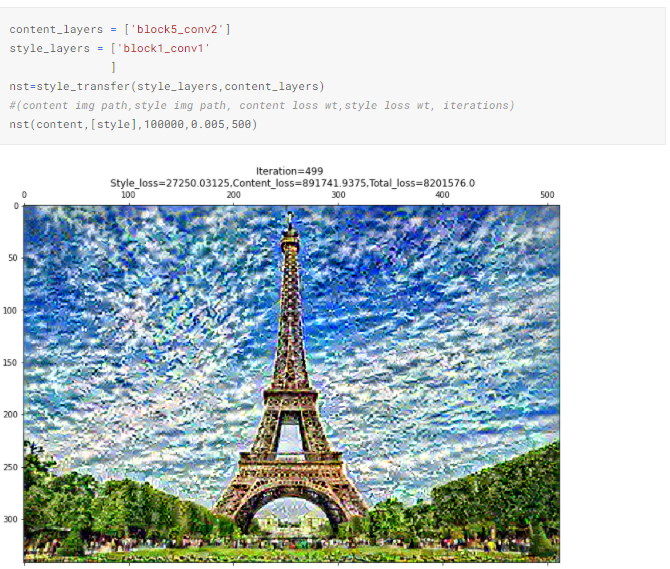
4.4 Using a different layer for content loss
Using block1_conv1 for content information forces the network to capture global features from the target content image. This probably interferes with the global features from the style image, and we end up getting an appalling style transfer. The result, I believe, demonstrates why it is encouraged to use deeper layers for NST. They focus solely on local details about prominent objects in the content image, enabling a smooth replication of the style image’s theme.
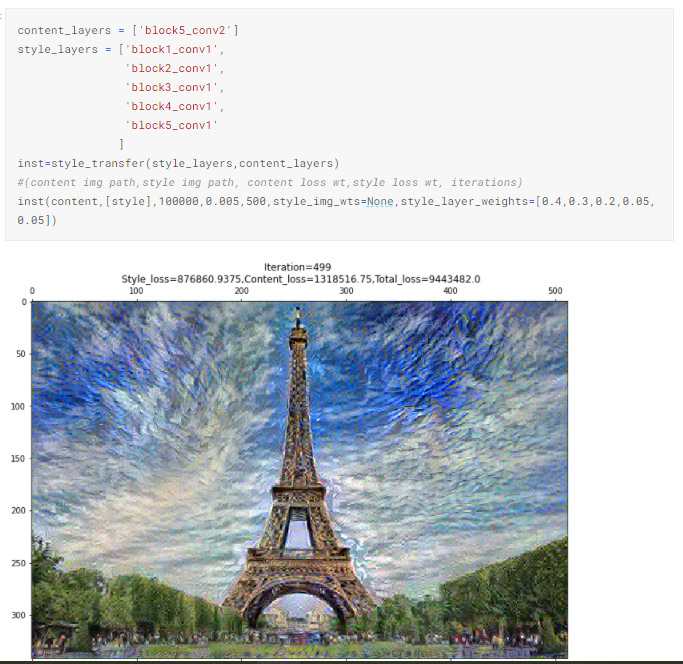
4.5 Manually assigning weights to style layers [0.4,0.3,0.2,0.05,0.05]
Although there’s not a discernible difference between 4.1 and the current recomposition, it seems to me that the latter has an overall light shade. This can be due to a higher weight assigned to block1_conv_1, which according to 4.3, generates a white tone from the Starry night painting.
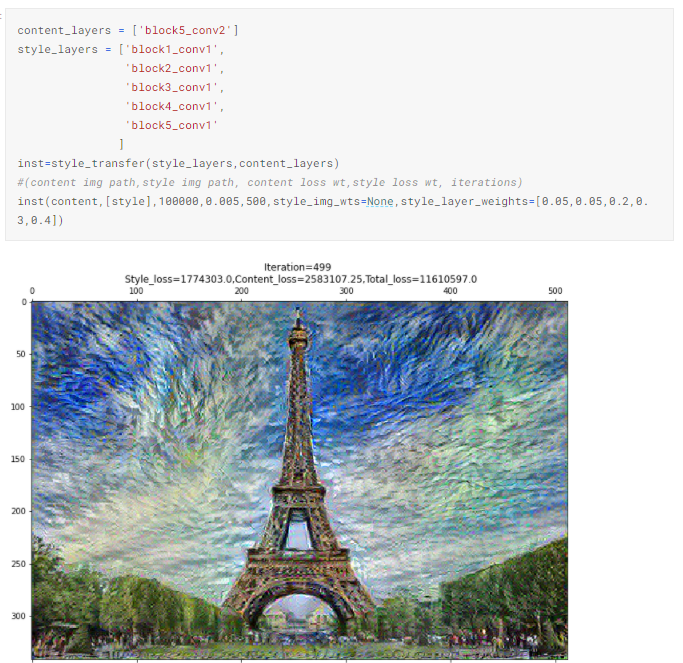
4.6 Manually assigning weights to style layers [0.05,0.05,0.2,0.3,0.4]
It has a more striking combination of colors compared to 4.5. Assigning higher weights to deeper layers provides more appealing results. Gram matrices from these layers are perhaps computing the correlation between more dominant global features from Starry Night.
4.7 Using multiple images for style transfer
Finally, let’s capture style from multiple images for more artistic recompositions. It entails a slight modification in style loss. Style loss for each image remains as discussed earlier in 3.2.2

However, the total style loss is:
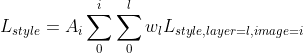
Essentially, as we have done so far, we assign weight to style loss from each image and sum them up.
5. Remarks
With that, I conclude the post. I urge you to carry out more experiments with the provided code. Also, I have implemented the algorithm from scratch, and there ought to be a more efficient procedure. A better optimizer certainly boosts the performance. I hope it was fun generating art using neural networks. Combining neural style transfer with generative adversarial networks is an enticing proposition, and I hope to cover it in the future.

References:
A neural algorithm of artistic style-Gatys et al
https://arxiv.org/abs/1508.06576
Notebook Links:
1.Kaggle:
NeuralStyleTransfer_experiments
2. Github
https://github.com/shashank14k/MyWork/blob/main/neuralstyletransfer-experiments.ipynb
AI for painting: Unraveling Neural Style Transfer was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/2ajCVht
via RiYo Analytics

No comments