https://ift.tt/31K97i6 Each convolution kernel is a classifier! An Intuitive Guide to Information Flow behind Convolution and Pooling Layer...
Each convolution kernel is a classifier! An Intuitive Guide to Information Flow behind Convolution and Pooling Layers
Dive deep into the meaning of numerical values in Convolutional Neural Networks and unveil how behind-the-scene information flows in-between Convolution and Pooling layers.

“AI is the new electricity” — Andrew Ng. It can be said the same for Deep Convolutional Neural Network (CNN) and Computer Vision: Convolutional Neural Network is the new electricity for Computer Vision.
CNNs are truly a diamond for the Machine Learning community, especially in the rapidly growing field of Computer Vision. They are the backbones of a myriad of fundamental tasks in computer vision, from as simple as image classification (but was considered very challenging or intractable just more than 2 decades ago) to more complicated tasks, including image segmentation, image super-resolution, and image captioning. This is why there has been a growing interest in CNN in both academics and industry in the past decade. Although many engineers and students are practicing and using CNNs on a day-by-day basis, most people lack a comprehensive theoretical view of Convolution and Pooling blocks, the two most basic building blocks of any CNN.
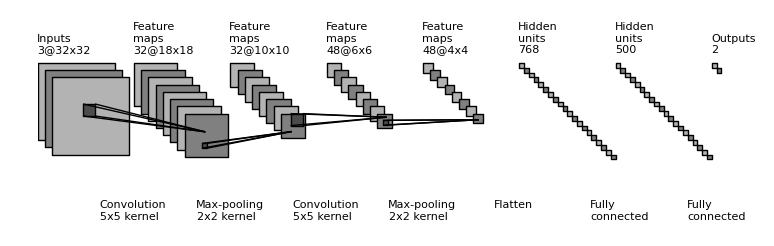
Having a solid theoretical view of CNNs, especially from Information Theory aspects, are particularly important to come up with novel ideas that significantly improve Deep Learning model’s capability on a specific task or even solve a problem with an efficiency that nobody has ever been able to. In the rest of this article, I will briefly introduce the concept of Information Theory and then explain in detail the meaning of numerical values in each layer of CNN from an Information Theory and Statistical point of view. I hope the content covered in this article will help you have a new way to see how CNNs work and come up with your own CNN model to solve your Computer Vision better, earn medals on Kaggle, or even end up publishing papers in top-notch conferences like CVPR and ICCV.
Information Theory in Deep Neural Network
You are probably familiar with the concept “feature extraction”, which is exactly all Convolution kernels are doing (in the simplest sense). However, have you ever tried to dive deeper to know more about “feature extraction”? To be specific, exactly what is being extracted, how does the convolving function do feature extraction a from numerical point of view? In the end, what in CNNs are just numbers, numbers, and numbers. Has your curiosity ever urged you to find the meaning and the relationships between those numbers in CNN layers?
Although I have come across the terminology “informational flow” many times in CNN-based papers, I have been struggling to find any paper or any book which covers the information theory, or at least its intuitive point of view, behind Convolutional Neural Network at satisfiable depth.
First, we will have a brief introduction to information theory.
1. Self Information
Suppose an event X=x has probability p of happening. Then we define the information value I of event x as follow:
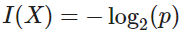
The meaning of value I is simply to measure how much / how valuable knowledge of event x happening is. The smaller the chance of happening p is, the higher the information value. Intuitively, when a rare event happens, people consider it to be more valuable; on the contrary, if an event is too common, we often consider it to contain not much information value.
For example, you know you have to go to work the next Monday (p = 0.99), then the knowledge that you have to go to work next Monday is actually useless because it does not change any of your current decision. However, if all of sudden your boss tells you that you have to go to Europe tomorrow for a very important business (p = 0.01), the information value is then very high, and it affects your current plan a lot.
2. Entropy
Self-information measures the information value of a single discrete event, while Entropy goes further to capture the information value of a random variable, whether it is discrete or continuous.
If a Random Variable X has p.m.f / p.d.f of p(x), then the Entropy is defined as followed:
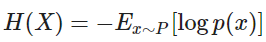
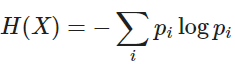
- If X is continuous:
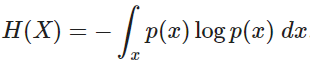
3. Conditional Entropy
Similarly, we define conditional entropy of random variable X and Y as follow:
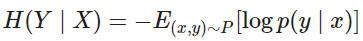
The conditional entropy measures the expected information value of knowing an event in Y happens, given that we know an event in X already happened. This property is particularly important as it is directly related to the information theory in Computer Vision at a level as low as pixel level.
4. Information Theory in Convolution Kernels
Almost any serious practitioner of CNN must already have a solid understanding of what convolution kernels do, including stride and feature extraction, at high-level understanding. If those concepts are unfamiliar to you, I highly recommend this great article for an introduction to convolutional neural network: Convolutional Neural Network.
In the next section, I will introduce the Information Theory of Convolution Kernels.
Convolution Kernels are Classifiers (surprise?)
1. Convolution review
The most common kernel size in modern CNNs are 3*3 kernels. Suppose we apply a single 3*3 kernel on the original RGB image, the total number of pixels observed in the receptive field would be 27 (H:3, W:3, C:3). Let the convolution kernel be function f, then f: R²⁷ → R. The input is the image part with 27 pixels, and the output is a scalar value.
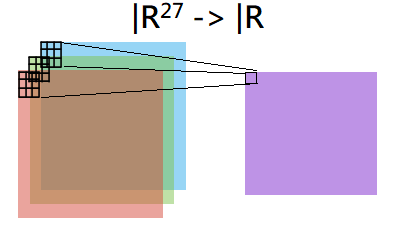
What is this outputted scalar value? What is the true meaning of this pixel that makes convolution operation work so efficiently on complex vision tasks?
2. Each kernel is a classifier
It is surprising that the outputted scalar is actually a relative probability. In other words, each convolution kernel is a classifier! This is the core idea of feature extraction!
Suppose kernel f: R²⁷ → R is responsible for extracting a feature k (edge, round objects, bright objects, etc.) We can rewrite kernel f as:
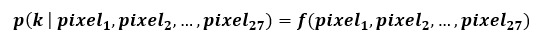
The intuitive description is that kernel f observes all 27 pixels in its receptive field, and learns to classify whether the “seen” area in the image contains feature k or not. Suppose k is “edge”, please look at the experiment and comments in Figure 1 below for a visual explanation.
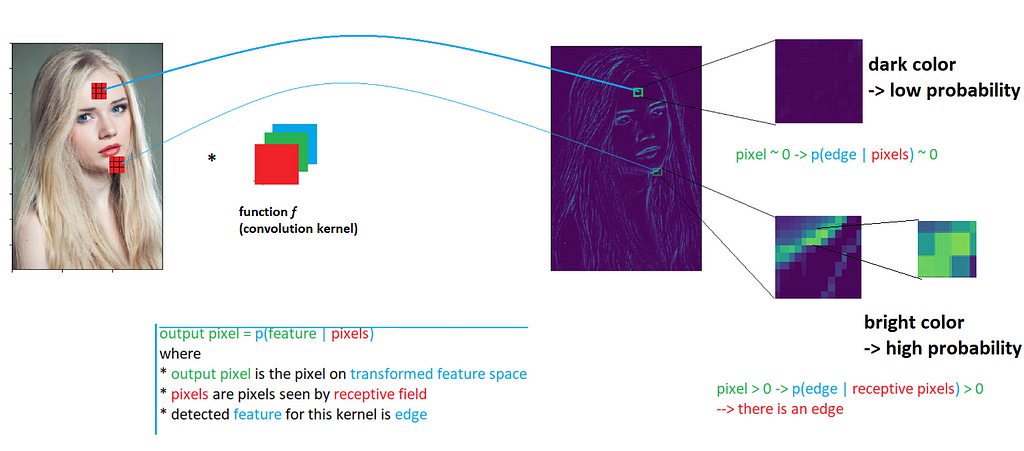
- Note: this is only the relative probability, meaning the outputted scalar can be any real number and may not be in the range [0,1]. For visualization of the extracted feature map, softmax transformation has been applied to convert values to exact probabilities.
To sum up, here are the core ideas of Convolution kernels from Information Theory aspects:
- Each convolution kernel is technically a classifier. It observes a set of pixels from the receptive field, and output a scalar measuring the probability that the image region in the receptive field contains kernel feature or not.
- A set of outputted probabilities are organized as pixels also makes the extracted features becomes visually visible to human eyes.
- The organization of outputted pixels p(feature k| pixels) corresponds to pixel locations in the original image. This keeps the overall structure and location of objects in the original image, and this explains how information flows between convolutional layers.
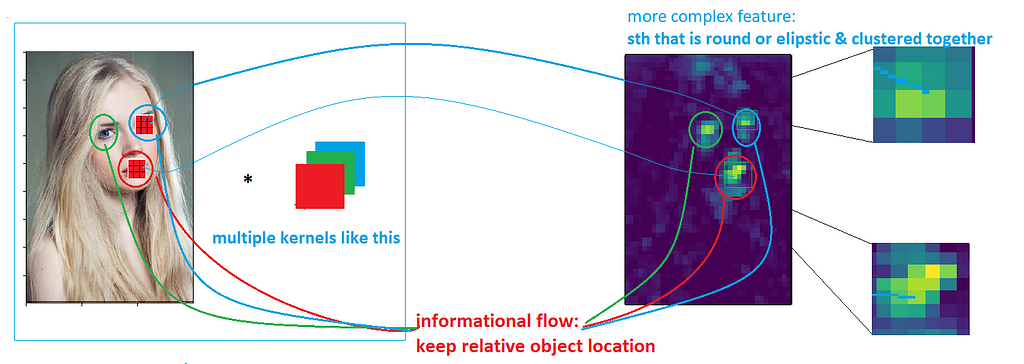
Intuitive View of Pooling Layer from Information Theory Aspects
Similar to Convolution Kernel, pooling can also be explained by Information Theory and Informational Flow.
Some benefits of pooling layer at high-level understanding:
- Dimensionality reduction for faster training and easier learning curve
- Increase information density and remove sparse distribution
Pooling layer from Information Theory aspects:
As presented in the earlier section, each pixel in the deep feature maps k is technically a relative probability that the corresponding region in the original image contains feature k. A high value indicates it is very likely the observed region has feature k, and vice versa.
Since images have sparse informational distribution by nature, and pooling layers are responsible for densifying distribution with minimal informational loss.
The Figure below helps clarify the information flow in-between pooling layers:
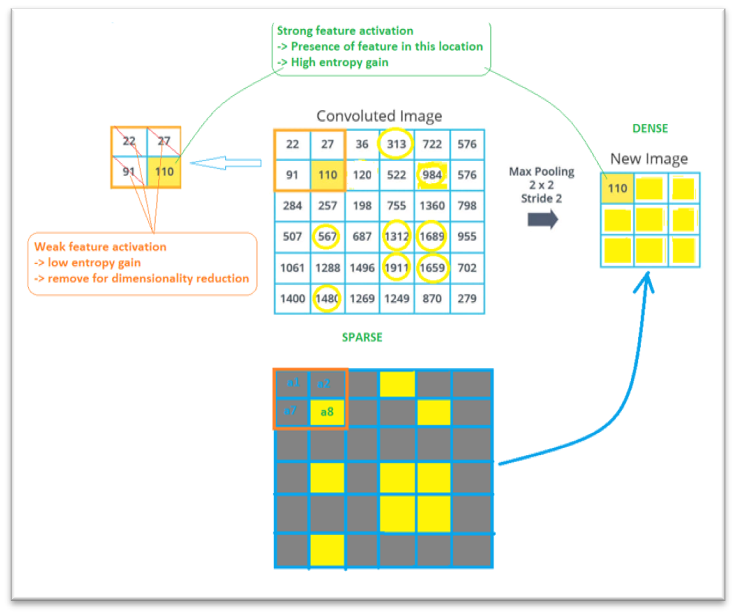
There is a natural concern regarding the removal of neighboring pixels (for instance, keeping a8 while removing a1, a2, a7): does it significantly affect the flow of information between layers and harm the CNN performance? The answer is that there certainly will be informational loss, but that is an acceptable loss to make each pixel in the feature map more meaningful. a1, a2, a7, a8 are neighboring pixels and tend to be correlated. As a result, the Entropy gain of those pixels combines is not significant, and we may need only 1 pixel to represent the information of those 4 pixels in the feature map. The Pooling layer filters the three less significant pixels, which are a1, a2, a7, and retains a8 as the only information to flow to deeper layers.
Discussions
Here is a list of follow-up questions that may help you understand the CNNs better from the Informational Flow and Information Theory point of view:
- What is the numerical meaning of addition in the residual connection? What information is transferred? Exactly why convolution may have informational loss? (hint: each convolution kernel can capture 1 specific feature, either simple or complex, and some sets of features do not overlap).
- Why do we use Max pooling and sometimes Average pooling? What are the benefits of Min pooling?
- Is the pooling layer considered the bottleneck of CNN, and why it is or it is not?
References
[1] Dive into Deep Learning book, Section 18.11: “Information Theory”:
Dive into Deep Learning — Dive into Deep Learning 0.17 documentation (d2l.ai)
[2] Understanding Convolutional Neural Networks with Information Theory: An Initial Exploration: 1804.06537.pdf (arxiv.org)
[3] Information Gain and Mutual Information for Machine Learning
[4] A Gentle Introduction to Information Entropy
[5] Convolutional Neural Network
Each convolution kernel is a classifier! was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3y9MoI0
via RiYo Analytics

No comments