https://ift.tt/3jldnum This is the third in a series of articles about Information Theory and its relationship to data driven enterprises a...
This is the third in a series of articles about Information Theory and its relationship to data driven enterprises and strategy. While there will be some equations in each section, they can largely be ignored for those less interested in the details and more in the implications. The prior article about Mutual Information & oddly the plot of MacBeth can be found here.
Causality is Overrated
Let’s create a situation. Suppose there was some random process, call it X. This process accepts some input (µ) and then produces an output based on a Cauchy distribution centered at µ. Cauchy distributions are troublesome because they look in almost every way like a normal distributions but with slightly higher likelihoods of extreme events (slightly fatter tails). The result is that while Normal processes have well defined expectations and vary in expected ways, Cauchy distributions have an undefined mean and vary infinitely wildly. Let’s define another process called Y. The result of the Y process is caused X such that:
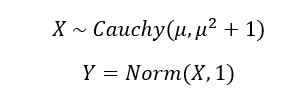
Y is caused by X and X is caused by µ. Knowing the input to X gives you almost no information about X, while knowing Y gives you modest information about X. If you want to know X you are much better off knowing the correlative information (Y) than the causal information (µ).
The focus on causality is driven in large part by a fear of spurious correlation[1] and putting too much faith in ephemeral relationships. To see this consider the following series generated by randomly selecting 1 and 0 at equal odds:

Without knowing the generating function Series 2 and 3 offer perfect information of each other. Of course there’s no guarantee this trend will continue — in fact it’s very unlikely to persist beyond 3 or 4 more digits. Put another way, we could make a simple rule: when series 2 presents a 1, series 3 presents a 0 and vice versa. In fact, any rule derived from these observations is guaranteed to eventually fail catastrophically as the series continue.
As the above example demonstrates its not crazy to be concerned with causality but it is somewhere between foolish to painfully stupid to only be concerned with it. Causality is notoriously difficult to prove, especially in the social sciences…especially in business settings. Consider the following set of sequential events:
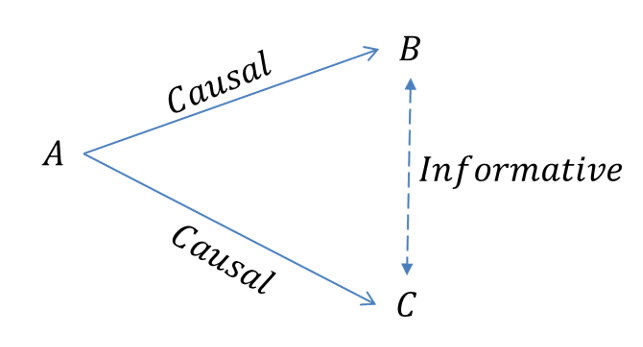
In the above diagram A is an instantiating event for events B & C. The outcome of A impacts B & C through some unknown, causal processes. In a panglossian world we would have perfect knowledge of event A, its outcomes and the process by which it causes B and/or C. Ours is not the best of all possible worlds though. A few reasons that we may not have access to this information include problems of:
1. Confidentiality: The scenario may be in some sense illegal to know about either the outcome of A or process for influencing B&C. See: secret information and materially important nonpublic Information as examples
2. Irreducible Complexity: The scenario may be so hopelessly complex that no one has the intellectual capacity[2] to understand either event A or the myriad of confounding factors and interactions in the causal process. See: public health and social psychology
3. Expense: The scenario may be incredibly expensive to understand, either in terms of direct cost, technology debt or time cost. See astrophysics (we tend not to visit far flung stars) and macroeconomics (we tend not to crash the economy to see what will happen)
If any of these apply all is not lost though. If A is causal of B we would expect it to hold considerable (or at least a non 0) amount of mutual information with B. Same for A & C. And since mutual information is symmetric:
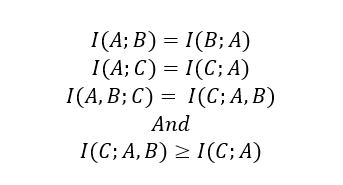
Put more succinctly, observing event B gives information about event C even though B is non-causal. But the situation is even better. Not only does B provide information about C in a correlative sort of way it even passes the sniff test because they are related through A. But wait, there’s more. If you have some historical data about the general relationship between A & B then it obviates the need to understand the complex causal processes linking A to either B or C.
Growth in sales and ARR are causal of price movement, though they are confidential ahead of an earnings call. The number of reviews left on their website is not confidential and while a review does not cause a sale, it may well provide information about the number of sales made (more sales -> more reviews presumably). Likewise, a Thursday night Seahawks game does not cause accidents on the factory floor, but may portend them. Causality is expensive and misleading, mutually informative events are inexpensive and useful.
The Disproportionate Information of Rare Events: A Gameification Crisis
Let’s start with a data science interview question. Usually, as part of an initial screening round for entry level candidate I like to find an example on their CV of a project that used real life data. Real life data is much nastier than academic and research data. Its chalked full of missing data, mixed (integer and string) data and outliers that make consuming and modeling the information grossly more difficult. Invariably most of the conversation revolves around these real world considerations. How do you handle missing data? Usual answers involve some sort of information replacement strategy like replace them with the average value of the column. Fair and reasonable. How do we deal with malformed or mixed data? Again usually a fair answer involving mapping strings to numbers. Finally what did you do about the large outlier events? Usually the answer is that they ‘removed them’ because you ‘can’t be expected to predict rare events.’ The ultimate justification: it improved the models accuracy. That’s good answer if building a forecast is a game or contest, much worse if you want to use it.
Outliers are intensely important. While it may be fair to remove them, we also must exercise caution in their treatment. We can see this from both an information theory and an intuitive perspective. As always let’s start with the theory. To begin let’s consider the partial entropy of an outcome.
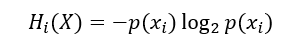
Partial Entropy is the amount of information a particular outcome has in a random process. The sum of partial entropy for each outcome is the entropy of the random process X.
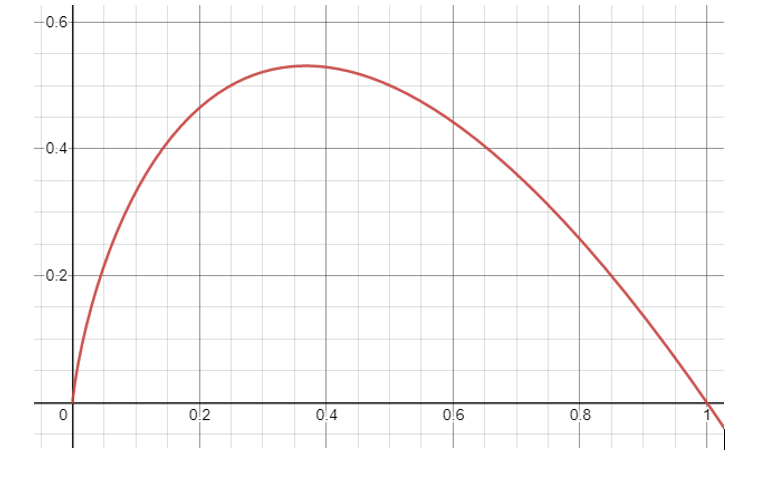
From the above graph we notice a few things. First, that information form outcomes is not symmetric. Outcomes with a 40% likelihood of occurring do not contain the same information as those with 60%. In fact partial entropy is skewed toward rarer events; an event with 40% probability contains more information than its 60% counterpart. This leads us to the second observation that rare events, those with near 0 probability, contain the same amount of information as very common events. Events with a 96.4% chance of occurring add about .05 bits of information roughly the same as an event with .7% chance of occurring. It would be unwise to ignore 96.4% of the world, it’s equally unwise to ignore the .7% of it.
The mechanics of callously ignoring rare events makes is an even more dangerous activity. Let’s consider a process X with outcomes A, B C such that:
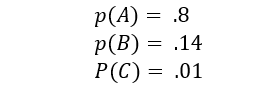
And let’s suppose we have 1000 observations that we are going to build our model on. The entropy of X is ~.72. let’s consider another metric that comes from entropy:

The Marginal Entropy of an Observation looks at the amount of information carried by a single observation. It is useful for assessing the impact of removing (ignoring) individual rows of data. By applying both marginal and partial entropy we can assess the impact of ignoring any portion of the data.

Individual observations about event C carry 3 times the information as event B, and 20x observations of A. You would not ignore observations about 80% (A) of your outcomes without good cause, and you should need a much better reason to ignore observations about C. Outcome C also contains 8% of the total amount of information in the data. While it may be ok to ignore 8% of the world, its worthwhile to be extraordinarily cautious.
Removing these events doesn’t just lose information, it also produces false confidence in your forecast. From the perspective of mutual information, a good forecast is one that maximized the mutual information between a model and the world. Once we remove rare events we are no longer modeling the world, but something else. We are modeling a gamified version of it, one where the goal isn’t risk-mitigation or return capture, but one where the goal is to get a high score. This may be good for instructive purposes but is terrible for marking well reasoned decisions.
Theory aside, the practice of removing extreme events should disturb our guts as well. The vast majority of car collisions involve fenders and bumpers at low speed. Love taps in dense traffic, backing into a beam in a parking lot, that sort of thing. If you remove the outliers, you end up ignoring the types of collisions you actually care about. Factories do not come to a grinding halt because the shipment arrived in the afternoon rather than the morning and economies don’t collapse due to the day to day variation in asset prices. Extreme events are events of both consequence and disproportionate information.
Information Risk: A Second Look
In the first article we briefly described a concept called information risk. Thus far we have discussed how, in an uncertain world, we can better understand uncertainty and how we can cope with it. We have also shown how malformed perceptions of certainty or over reliance of ‘causality’ can be at best detrimental and at worst catastrophically wrong. Information Risk in these scenarios largely means being overly confident when we shouldn’t be. In the next section we will look at what happens when even deterministic systems — those with perfect mutual information between observations and outcomes — become more complex than we can hope to understand.
— — — — — — — — — — — — — — — — — — — — — — — — — — —-
[1] And something called the No Free Lunch Theorem
[2] We will treat this in a future article as ‘channel capacity’
Information Theory: Principles and Apostasy was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3m0E5Kl
via RiYo Analytics

No comments