https://ift.tt/2ZCFvSM Parts of speech are useful clues to sentence structure and meaning. Here’s how we can go about identifying them. Th...
Parts of speech are useful clues to sentence structure and meaning. Here’s how we can go about identifying them.
The complete code for this article can be found HERE
Part of speech tagging is the process of assigning a part of speech to each word in a text, this is a disambiguation task and words can have more than one possible part of speech and our goal is to find the correct tag for the situation.
We will use a classic sequence labeling algorithm, the Hidden Markov Model to demonstrate, sequence labeling is a task in which we assign to each word x1 in an input word sequence, a label y1, so the output sequence Y has the same length as the input sequence X. An HMM is a probabilistic sequence model based on augmenting the Markov chain. A Markov chain makes a very strong assumption that if we want to predict the future in the sequence, all that matters is the current state. For example, predicting the probability that I write an article next week depends on me writing an article this week and no more. You can watch the video HERE for more examples and I would say a more detailed explanation.
The Hidden Markov Model allows us to talk about observed events — words that we see in the put and hidden events — part of speech tags that we think of as casual factors in our probabilistic model.
We will be implementing our tagger using the Brown Corpus where each file contains sentences of tokenized words followed by POS tags and where each line contains a sentence. You can find the manual for our data describing the tags HERE. Note we will implement our POS tagger using a bigram HMM.
We can see a sample of our data below:
[('RB', 'manifestly'), ('VB', 'admit')]
First, let's create a function for generating n-grams.
def ngrams(self, text, n):
n_grams = []
for i in range(len(text)): n_grams.append(tuple(text[i: i + n]))
return n_grams
Transition probabilities
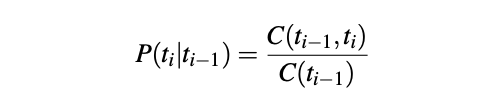
An HMM has two components that transition probabilities A and emission probabilities B.
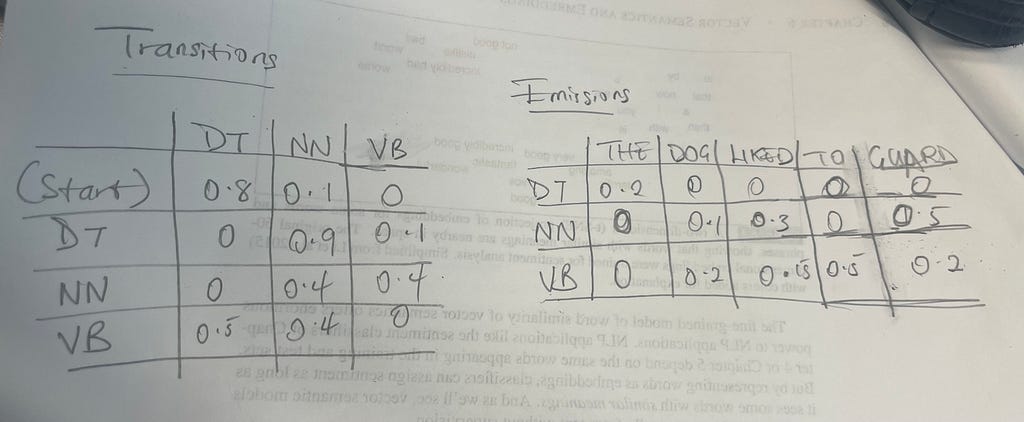
The transition probabilities are the probability of a tag occurring given the previous tag, for example, a verb will is most likely to be followed by another form of a verb like dance, so it will have a high probability. We can calculate this probability using the equation above, implemented below:
Here we are dividing the count of the bigram by its unigram count for each bigram we create and store it in a transition_probabilities dictionary.
Emission probabilities
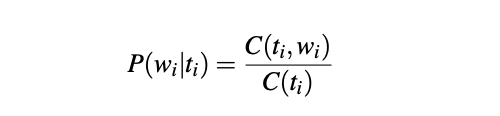
The emission probabilities are the probability given a tag that it will be associated with a given word. We can calculate this probability using the equation above, implemented below:
Here we are dividing the count of the tag followed by that word by a count of the same tag and storing it in an emission_probabilities dictionary.
HMM taggers make two further simplifying assumptions. The first is that the probability of a word appearing depends only on its own tag and is independent of neighboring words and tags, second assumption, the bigram assumption, is that the probability of a tag is dependent only on the previous tag, rather than the entire tag sequence. Plugging the two assumptions results in the following equation for the most probable tag sequence from our bigram tagger:
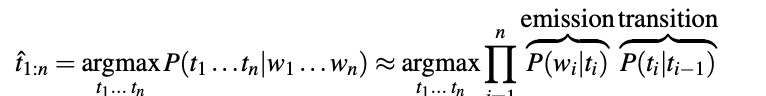
Decoding HMM
For any model, such as an HMM that contains hidden variables — the parts of speech, the task of determining the sequence of the hidden variable corresponding to the sequence of observations is called decoding, and this is done using the Viterbi algorithm.
Viterbi algorithm
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states — called the Viterbi path — that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models (HMM). Also, a good explanatory video can be found HERE
Viterbi decoding efficiently determines the most probable path from the exponentially many possibilities. It finds the highest probability given for a word against all our tags by looking through our transmission and emission probabilities, multiplying the probabilities, and then finding the max probability. We will define a default value of 0.0000000000001 for unknown probabilities.
We will start by calculating our initial probabilities / the start probability for that state, this is the probability that the word started the sentence, in our case we used a “START” token
def initial_probabilities(self, tag):
return self.transition_probabilities["START", tag]
Testing
To test our solution we will use a sentence already broken into words, as below:
test_sent = ["We",
"have",
"learned",
"much",
"about",
"interstellar",
"drives",
"since",
"a",
"hundred",
"years",
"ago",
"that",
"is",
"all",
"I",
"can",
"tell",
"you",
"about",
"them",
]
cleaned_test_sent = [self.clean(w) for w in test_sent]
print(self.vertibi(cleaned_test_sent, all_tags))
Our result i:
we,PPSS
have,HV-HL
learned,VBN
much,AP-TL
about,RB
interstellar,JJ-HL
drives,NNS
since,IN
a,AT
hundred,CD
years,NNS
ago,RB
that,CS
is,BEZ-NC
all,QL
i,PPSS
can,MD
tell,VB-NC
you,PPO-NC
about,RP
them,DTS
This is correct based on our documentation.
I look forward to hearing feedback or questions.
Implementing Part of Speech Tagging for English Words Using Viterbi Algorithm from Scratch was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Towards Data Science - Medium https://ift.tt/3vUDayk
via RiYo Analytics

ليست هناك تعليقات